Где используется трапеция в жизни: История трапеции и применение в жизни
«Мир четырёхугольников» — математика, прочее
Районный конкурс ученических
проектов по математике
«Юный исследователь»
Муниципальное бюджетное общеобразовательное учреждение Жирятинская средняя общеобразовательная школа им.А.Ф.Возликова
Название работы:
Мир четырехугольников
Работу выполнили:
Исаева Вера
Молодожен Лидия Сёмина Анастасия
Гузенкова Светлана
Руководитель :Козлова Галина Петровна, учитель математики
Адрес школы:
с.Жирятино ул.Ленина д.38
Жирятино
2018
ОГЛАВЛЕНИЕ.
1.Введение………………………………………………3
2.Цели и задачи…………………………………………3
Основное содержание…………………………………4
2. 1 Определение четырехугольника ………………… 4
1 Определение четырехугольника ………………… 4
2.2 Таблица классификации четырёхугольников……5…
2.3 Параллелограмм………………………………5
2.4 Ромб………………………………
2.5 Прямоугольник………………………………
2.6 Квадрат………………………………
2.7 Трапеция………………………………
2.8 Ортодиагональный четырёхугольник…………………
Заключение…………………………………………………………12
Библиографический список………………………………………..13
I. Введение Актуальность темы: Нам порою кажется, что геометрия совершенно не связана с нашей жизнью, что это очень трудная и совсем непонятная наука. Часто самые интересные факты — из-за малого количества отведенных на предмет часов — проходят мимо вас. На самом же деле мы с вами живем в мире, который неразрывно связан с геометрией. В ходе работы над проектом перед нами открылся удивительный мир четырёхугольников, обладающих неповторимыми свойствами. Квадраты, ромбы, прямоугольники… каждый ученик сталкивается с ними в школе на уроках геометрии. Основополагающий вопрос: Можно ли представить себе мир без четырехугольников? Зачем мы изучаем четырехугольники? Какое применение находят четырехугольники в природе и технике? Что связывает четырехугольники между собой? Чем интересны четырехугольники? Научная формулировка гласит, что геометрия — это раздел математики, который изучает фигуры и свойства фигур на плоскости и в пространстве . Стоит осмотреться, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. В современной архитектуре смело используются самые разные геометрические формы, чаще всего – четырехугольники. Плитки пола в ванной, на тротуарах, на вокзалах чаще бывают четырехугольными. По улице движутся автомобили, автобусы, троллейбусы, их окна это четырехугольники: трапеции, квадраты, прямоугольники. Цель работы – Провести классификацию четырехугольников, систематизировать знания для подробного изучения темы «Четырехугольники»; уметь применять теоретические знания в решении практических, занимательных задач, активизировать познавательную деятельность и интерес к геометрии.
Стоит осмотреться, и мы увидим, что многие предметы имеют форму, похожую на уже знакомые нам геометрические фигуры. В современной архитектуре смело используются самые разные геометрические формы, чаще всего – четырехугольники. Плитки пола в ванной, на тротуарах, на вокзалах чаще бывают четырехугольными. По улице движутся автомобили, автобусы, троллейбусы, их окна это четырехугольники: трапеции, квадраты, прямоугольники. Цель работы – Провести классификацию четырехугольников, систематизировать знания для подробного изучения темы «Четырехугольники»; уметь применять теоретические знания в решении практических, занимательных задач, активизировать познавательную деятельность и интерес к геометрии.
Исходя из цели, были поставлены следующие задачи:
1. Рассмотреть определения четырехугольников .
2. Изучить виды, свойства, признаки четырехугольников.
3. Выяснить, в каких областях человеческой деятельности применяются четырехугольники.
Объект исследования: геометрические фигуры четырехугольники.
Методы исследования:
2. Основное содержание
2.1 Определение четырехугольника.
Четырёхугольником называется фигура, которая состоит из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три из данных точек не должны лежать на одной прямой, а соединяющие их отрезки не должны пересекаться. Каждый четырехугольник имеет четыре вершины, четыре стороны и две диагонали. [1,19]. В курсе геометрии мы изучали выпуклые многоугольники: Параллелограмм, Ромб, Прямоугольник, Квадрат, Трапецию.
2.2 Таблица классификации четырёхугольников
Невыпуклые
Выпуклые
Прямоугольник
Прямоугольная
Квадрат
2. 3 Параллелограмм
3 Параллелограмм
Я- параллелограмм
В ажнее всех фигур,
Я всех их свойствами своими наделил.
Хоть стороны мои попарно и равны, и параллельны,
Всё ж я в печали, что не равны мои диагонали,
Да и углы не делят пополам.
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны.
Свойства:
1.Противоположные стороны параллелограмма равны и противоположные углы равны.
2.Диагонали параллелограмма точкой пересечения делятся пополам.
Признаки:
Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм
Если в четырехугольнике две стороны попарно равны, то этот четырехугольник – параллелограмм.
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм. [1,15].
[1,15].
Сумма любых двух соседних углов параллелограмма равна 180°:
Каждая диагональ делит параллелограмм на два равных треугольника. [4,7].
2.4 Ромб
А я — особый параллелограмм,
В се стороны мои наклонены,
да и к тому же все равны.
Меня за это ромбом величают.
Геометрической фигурой называют.
Диагонали под прямым углом пройдут.
На части равные фигуру разобьют.
Ромб – параллелограмм, у которого все стороны равны. Ромб является параллелограммом, значит, он обладает всеми свойствами параллелограмма.
Свойство:
Диагонали ромба взаимно перпендикулярны и делят его углы пополам, т.е. диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
Признаки:
1) Если у параллелограмма диагонали взаимно перпендикулярны, то он является ромбом.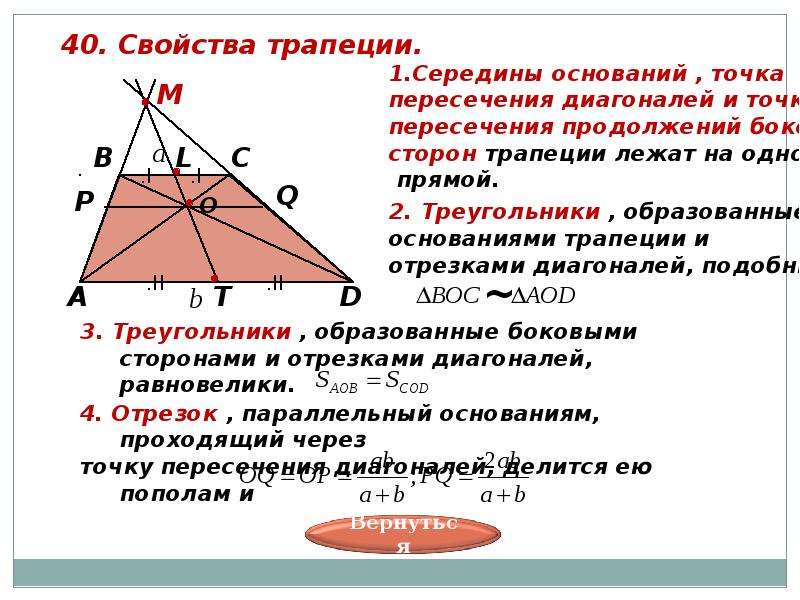
2) Если диагональ параллелограмма является биссектрисой его углов, то он является ромбом.
3) Если у четырехугольника все стороны равны, то он является ромбом.
4) Если смежные стороны параллелограмма равны, то он является ромбом.
2.5 Прямоугольник A я — прямоугольник,
В отличие от всех.
Все стороны свои держу я строго,
Две — чуть поменьше, ну а две побольше,
Которые напротив — те равны,
А те, что смежные, углом прямым скрепляю,
И преимущество имею я:
«Ведь всё ж равны мои диагонали».
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойство:
Диагонали прямоугольника равны
Признак: Если в параллелограмме диагонали равны, то этот параллелограмм — прямоугольник.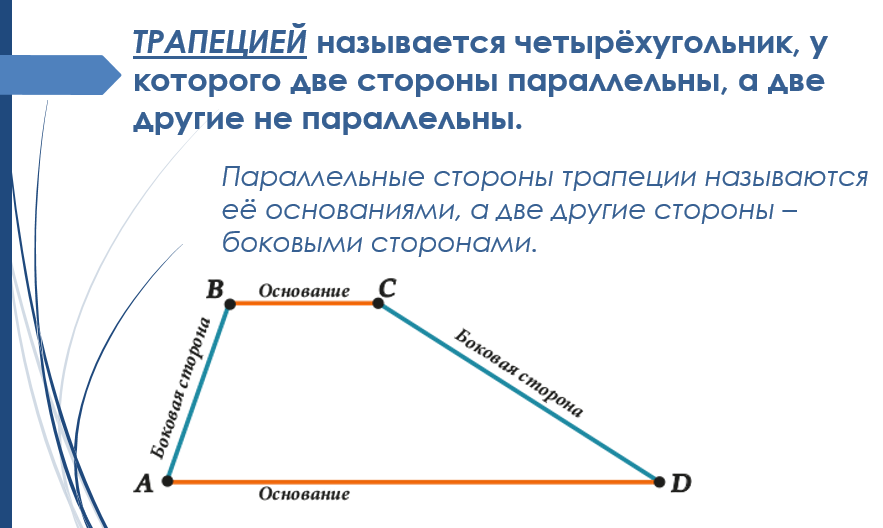
2.6 Квадрат
Р екомендуюсь: я — квадрат.
Любую площадь я измерить рад.
С глубокой древности я — мера площадей,
Она в квадрате стороны моей.
Имею я четыре стороны,
И все они равны.
Но у меня притом равны диагонали,
Углы они мне делят пополам,
На части равные разбит я ими сам.
Вобрав всё важное в себя,
Фигурой знатной стал и я
Квадрат – это прямоугольник, у которого все стороны равны.
Свойства: Квадрат обладает всеми свойствами ромба и прямоугольника.
1.Все углы квадрата прямые.
2.Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся полам, делят углы квадрата пополам.
2.7 Трапеция
А я — фигура, не похожая на всех
. Хоть я и не параллелограмм, Но среди всех фигур мне место есть.
Хоть я и не параллелограмм, Но среди всех фигур мне место есть.
Ведь у меня же параллельны основания.
Бывают стороны равны, диагонали.
Ещё углы при основании…
Тогда трапецией я равнобедренной зовусь.
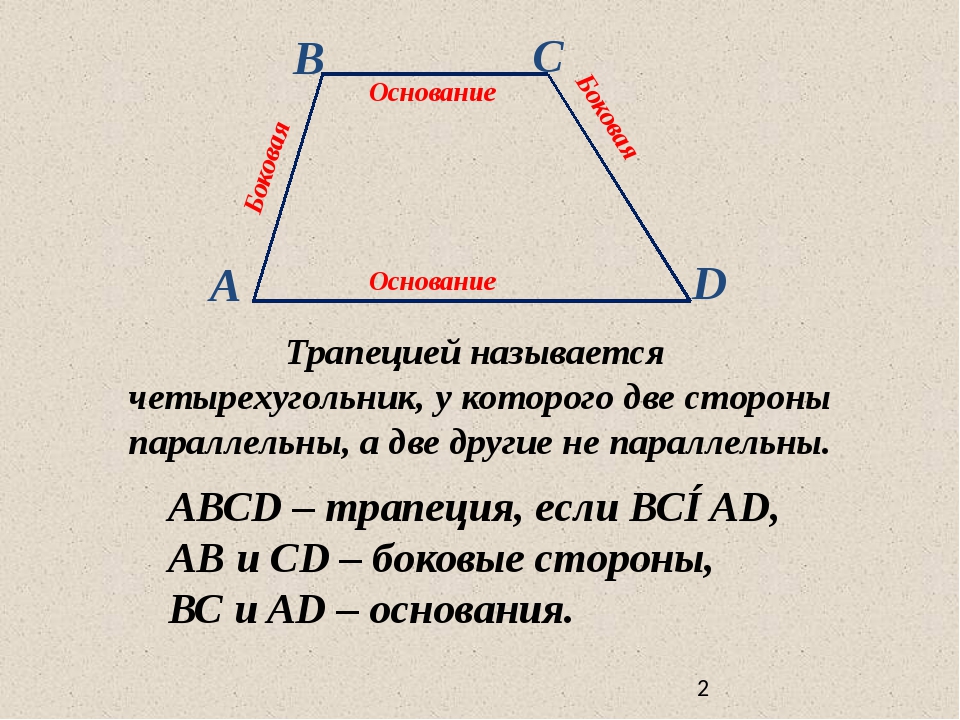
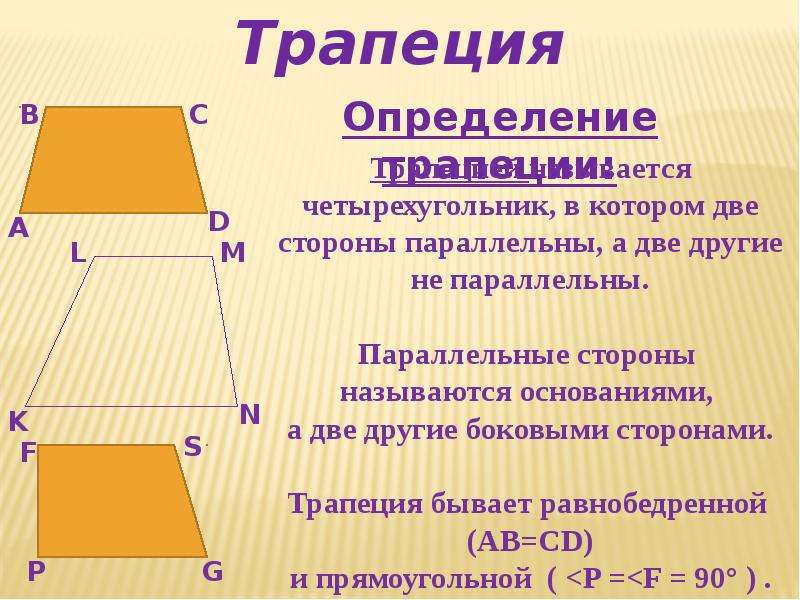
Трапецией называется четырёхугольник, у которого две стороны параллельны, а две стороны не параллельны.
Параллельные стороны трапеции называются основаниями, а две другие – боковыми. Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
Средней линией (первой средней линией) трапеции называется отрезок, который соединяет середины боковых сторон данной трапеции: Средняя линия трапеции параллельна её основаниям и равна их полусумме.
У равнобокой трапеции:
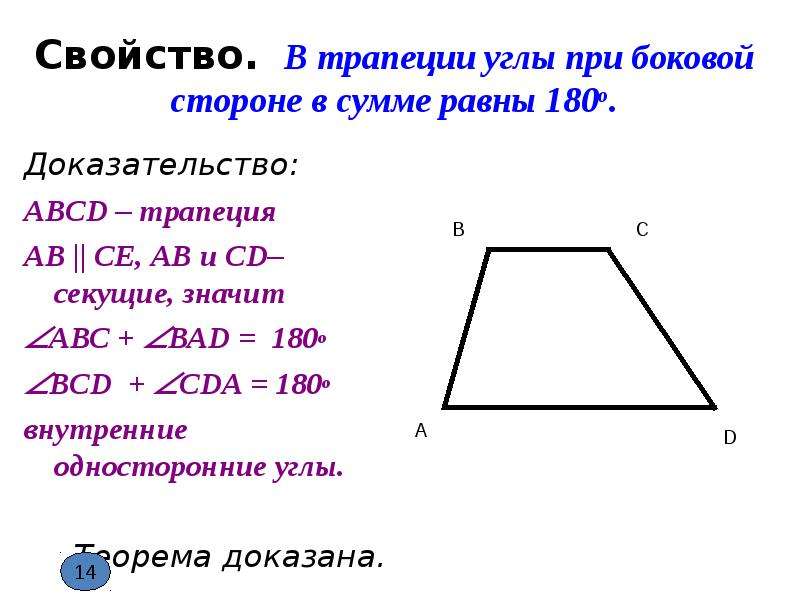
сумма противолежащих углов равна 180
Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.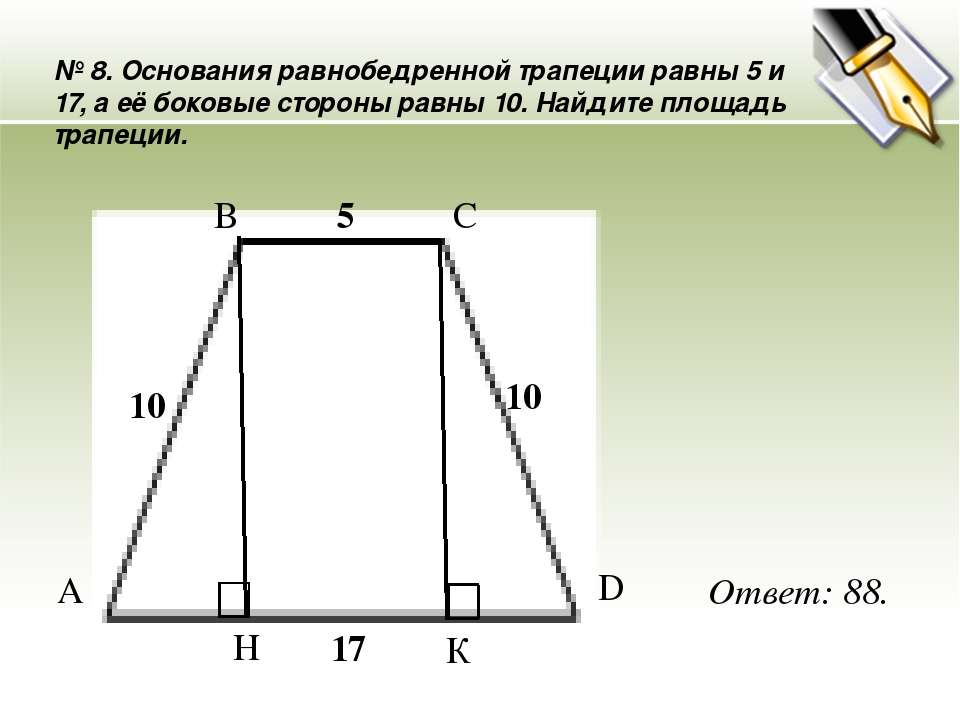
2.8 Ортодиагональный четырёхугольник
Изучая дополнительную литературу мы выяснили, что существуют другие виды четырёхугольников
Ортодиагональный четырёхугольник — это четырёхугольник, в котором диагонали пересекаются под прямым углом.
. Согласно описанию этих четырёхугольников, два красных квадрата на двух противоположных сторонах четырёхугольника дают в сумме ту же площадь, что и два синих квадрата на другой паре сторон.
Специальные случаи
Дельтоид является ортодиагональным четырёхугольником, в котором одна диагональ является осью симметрии. Дельтоиды — это в точности ортодиагональные четырёхугольники, имеющие окружность, касающуюся всех четырёх сторон. Таким образом, дельтоиды являются описанными ортодиагональными четырёхугольниками[1].
Ромб — это ортодиагональный четырёхугольник с двумя парами параллельных сторон
2. 8 Практическое применение четырехугольников в решении реальных задач.
8 Практическое применение четырехугольников в решении реальных задач.
3.Немного истории
Работая над проектом, мы нашли интересные факты о некоторых четырёхугольниках
Французский математик Франсуа Лукас (1847-1891)- специалист в области теории чисел, занимаясь поиском простого объяснения формы арабских цифр, столкнулся с легендой о перстне царя Соломона.
Легенда гласит, что на драгоценном камне, украшавшем перстень, была изображена таинственная фигура, квадрат с двумя диагоналями, из которой, можно получить фигуры всех десяти цифр
В средние века и в эпоху Возрождения математики были заворожены числом = 1.61803398…, названным «божественной пропорцией». Среди фигур — «золотой прямоугольник»..(В нём отношение большей стороны к меньшей равно числу 1.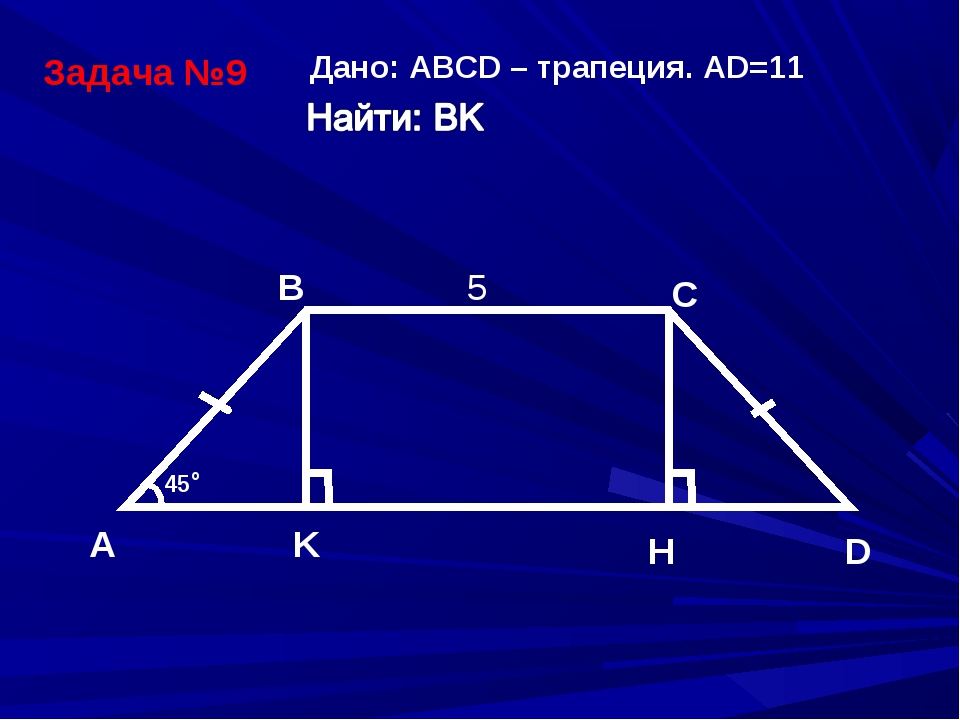 618
618
Демонстрация этой фигуры и её свойств:
Золотой прямоугольник сечения делится на квадрат и другой, меньший золотой прямоугольник сечения. Этот процесс может быть продолжен до бесконечности, добавляя квадрат (площадь) по более длинной стороне золотого прямоугольника сечения.
Окна, рамы картин, здания, книги часто приблизительно соответствуют Золотому прямоугольнику.
Парфенон V в. до н.э. одно из красивейших сооружений древнегреческой архитектуры.
Правило золотого сечения просматривается в фасаде здания.
4.Занимательная игра «Пифагор» Чтобы дать пищу нашему мозгу, человек издавна изобретает различные занимательные игры. Давайте рассмотрим некоторые математические игры. Вот, например, китайская игра «Танграм», она же греческая игра «стомахион». У нас можно встретить игру «Пифагор».
Ими увлекались ещё Архимед, французский император Наполеон.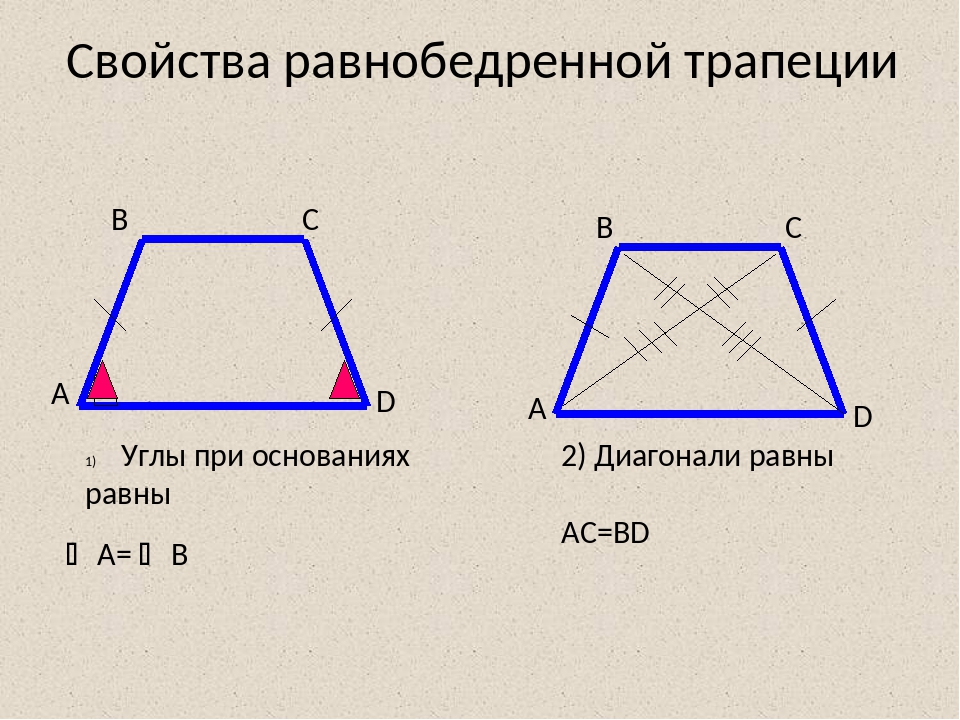
Описание игры. Квадрат размером 7X7 см разрезан так, что получается 7 геометрических фигур: 2 разных по размеру квадрата, 2 маленьких треугольника, 2 — больших (в сравнении с маленькими) и 1 четырехугольник (параллелограмм).
Цель игры состоит в составлении из 7 геометрических фигур — частей игры, плоских изображений: силуэтов строений, предметов, животных.
4. Заключение
Работая над проектом, наблюдая за окружающим миром мы выяснили, что четырехугольники окружают нас повсюду и играют важную роль в нашей жизни: определяют форму столь необходимых нам предметов, приборов и механизмов, радуют глаз, красуясь на фасадах памятников архитектуры и исторических сооружений, помогают в построении планов и схем, делают наш быт и повседневность проще, легче и удобней.
Вывод: Четырёхугольники – просто, сложно, интересно!
5. Список использованных источников
Список использованных источников
Интернет-ресурсы
http://images.astronet.ru/pubd/2003/03/15/0001187674/file0013.gif
http://www.peoples.ru/science/mathematics/pifagor
http://th-pif.narod.ru/biograph.htm
http://ru.wikipedia.org – Википедия – свободная энциклопедия
http://www.nigma.ru – интеллектуальная поисковая система
Атанасян Л.С. Геометрия 7-9: учеб. Для общеобразоват. Учреждений – М.: Просвещение, 2013
Большая энциклопедия Кирилла и Мефодия – 2010
Глейзер Г.И. «История математики»
9. Энциклопедия. Я познаю мир. Математика. – М.: ООО «Издательство АСТ», 2003. – 408 с.
14
Разница между Трапецией и Параллелограммом — Разница Между
Разница Между 2021
Ключевая разница: Трапеция представляет собой четырехугольник, который имеет по меньшей мере одну пару параллельных сторон.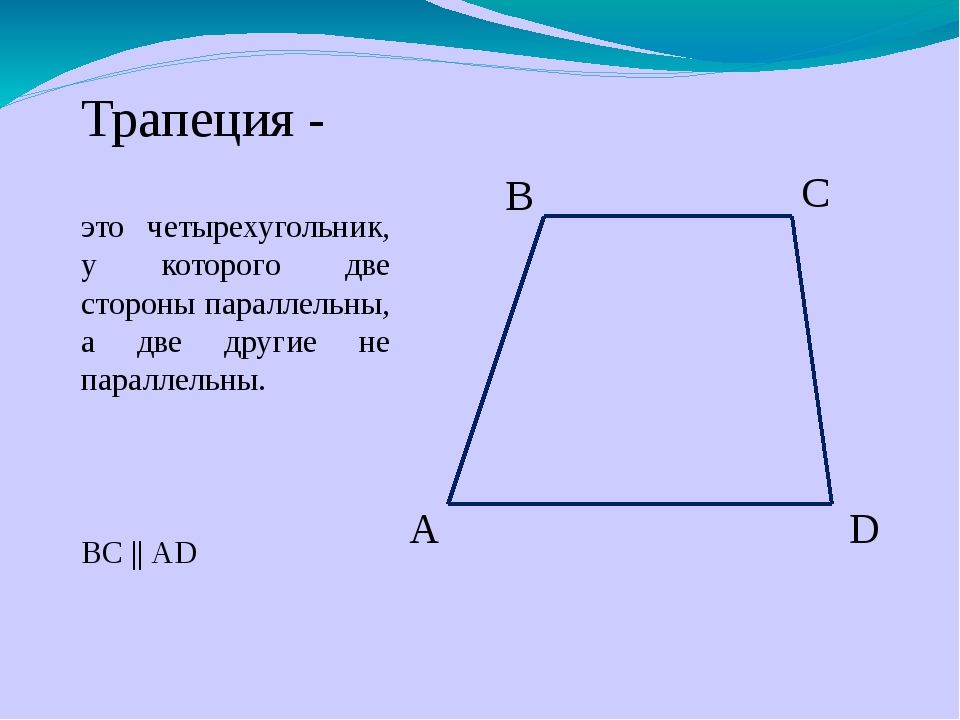 Эта фигура более известна как трапеция. Параллелограмм — это четырехугольник
Эта фигура более известна как трапеция. Параллелограмм — это четырехугольник
Содержание:
Ключевая разница: Трапеция представляет собой четырехугольник, который имеет по меньшей мере одну пару параллельных сторон. Эта фигура более известна как трапеция. Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Слова трапеция и параллелограмм обычно встречаются в математике и геометрии. Эти термины относятся к геометрическим формам, которые обычно используются для изучения и понимания углов. И трапеция, и параллелограмм являются четырехугольниками и могут привести к путанице для людей, которые активно не используют геометрию. Эти фигуры также играют важную роль в архитектуре.
Трапеция представляет собой четырехугольник, который имеет по меньшей мере одну пару параллельных сторон. Эта цифра широко известна как трапеция в большинстве стран мира, но в некоторых странах, таких как Великобритания, она называется трапецией.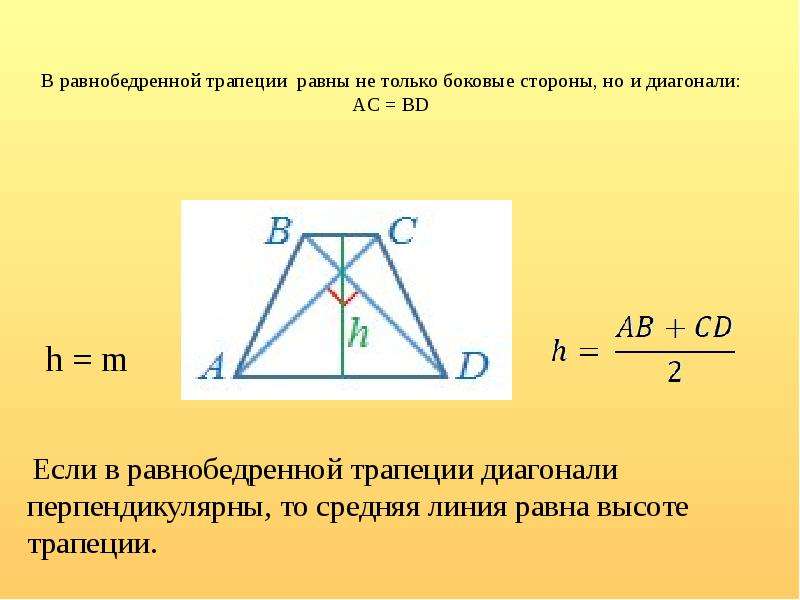 Согласно справке Math Open, название предполагает другие отличия. Трапеция в Соединенных Штатах относится к четырехугольнику без параллельных сторон, в то время как трапеция относится к четырехугольнику, который имеет одну пару параллельных сторон. Тем не менее, в Великобритании это считается противоположным; трапеция считается четырехугольником без параллельных сторон, а трапеция считается четырехугольником с одной парой параллельных сторон.
Согласно справке Math Open, название предполагает другие отличия. Трапеция в Соединенных Штатах относится к четырехугольнику без параллельных сторон, в то время как трапеция относится к четырехугольнику, который имеет одну пару параллельных сторон. Тем не менее, в Великобритании это считается противоположным; трапеция считается четырехугольником без параллельных сторон, а трапеция считается четырехугольником с одной парой параллельных сторон.
Параллельные стороны трапеции / трапеции называются основаниями трапеции, а две другие стороны называются ножками или боковыми сторонами. Однако, если боковые стороны ног параллельны, то трапеция будет иметь два основания. Существует некоторое несогласие с фактическим определением трапеции, при этом некоторые говорят, что трапеция имеет ровно одну пару параллельных сторон, в то время как другие определяют трапецию, имеющую по крайней мере одну пару параллельных сторон. Согласно первому определению, параллелограмм не будет рассматриваться как трапеция, тогда как во втором определении говорится, что параллелограмм будет особой разновидностью трапеции.
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон. Противоположные стороны параллелограмма параллельны друг другу, поэтому в названии есть параллель. Противоположные стороны параллелограмма имеют одинаковую длину, а противоположные углы параллелограмма имеют равную меру. Четырехугольник состоит из квадрата, прямоугольника и ромба. Прямоугольник — это параллелограмм с двумя парами параллельных сторон, которые образуют четыре прямых угла равных сторон. Квадрат — это параллелограмм с четырьмя сторонами равной длины и четырьмя прямыми углами одинакового размера. Ромб — это параллелограмм с четырьмя сторонами равной длины.
трапеция | Параллелограмм | |
Тип | четырехугольник | четырехугольник |
Ребра и вершины | 4 | 4 |
характеризации |
|
|
свойства |
Свойства равнобедренной трапеции (особый тип трапеции).
|
|
Формулы (mathopenref.com) | Площадь: (База 1 + База 2) / 2 х высота Нахождение высоты от площади: (2 х области) / База 1 + База 2 Нахождение базы из области: (2 х площадь / высота) — база | Периметр: 2 (ширина + высота) |
Какими свойствами обладает трапеция. Полезные свойства трапеции. Свойства средней линии трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции
.
Данный отрезок параллелен основаниям трапеции
.
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными
.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны
, то есть треугольники являются равновеликими.
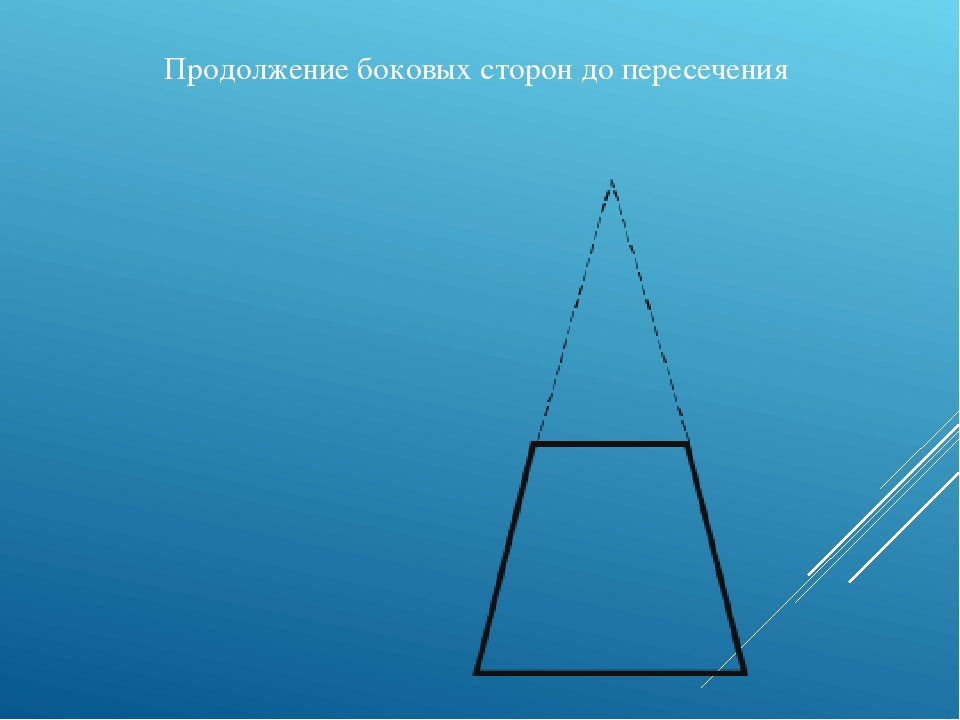
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований
.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции
(BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка
, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b
— основания трапеции
c, d
— боковые стороны трапеции
d1 d2
— диагонали трапеции
α β
— углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2
. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3
. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Примечание
. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме
.
Задача
.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение
.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ
: 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ
: площадь трапеции равна 80 см 2 .
С такой формой как трапеция, мы встречаемся в жизни довольно часто. К примеру, любой мост который выполнен из бетонных блоков, является ярким примером. Более наглядным вариантом можно считать рулевое управление каждого транспортного средства и прочее. О свойствах фигуры было известно еще в Древней Греции
, которую более детально описал Аристотель в своем научном труде «Начала». И знания, выведенные тысячи лет назад актуальны и по сегодня. Поэтому ознакомимся с ними более детально.
Вконтакте
Основные понятия
Рисунок 1. Классическая форма трапеции.
Трапеция по своей сути является четырехугольником, состоящим из двух отрезков которые параллельны, и двух других, которые не параллельны. Говоря об этой фигуре всегда необходимо помнить о таких понятиях как: основания, высота и средняя линия. Два отрезка четырехугольника которые друг другу называются основаниями (отрезки AD и BC). Высотой называют отрезок перпендикулярный каждому из оснований (EH), т. е. пересекаются под углом 90° (как это показано на рис.1).
е. пересекаются под углом 90° (как это показано на рис.1).
Если сложить все градусные меры внутренних , то сумма углов трапеции будет равна 2π (360°), как и у любого четырехугольника. Отрезок, концы которого являются серединами боковин (IF) именуют средней линей.
Длина этого отрезка составляет сумму оснований BC и AD деленную на 2.
Существует три вида геометрической фигуры: прямая, обычная и равнобокая. Если хоть один угол при вершинах основания будет прямой (например, если ABD=90°), то такой четырехугольник называют прямой трапецией. Если боковые отрезки равны (AB и CD), то она называется равнобедренной (соответственно углы при основаниях равны).
Как найти площадь
Для того, чтобы найти площадь четырехугольника
ABCD пользуются следующей формулой:
Рисунок 2. Решение задачи на поиск площади
Для более наглядного примера решим легкую задачу. К примеру, пускай верхнее и нижнее основания равны по 16 и 44 см соответственно, а боковые стороны – 17 и 25 см.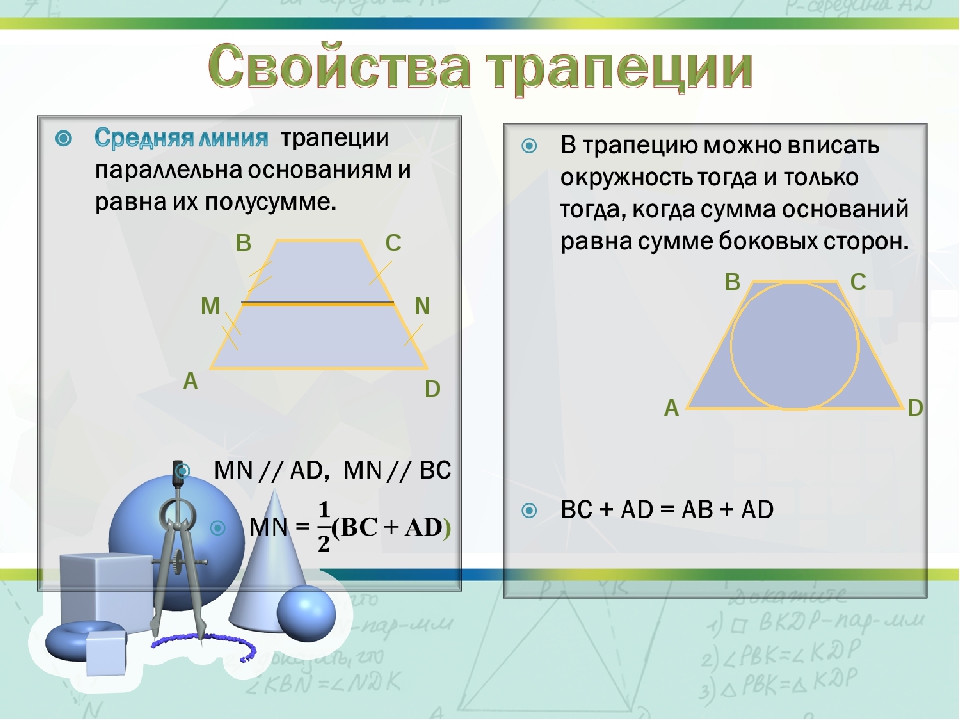 Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Построим перпендикулярный отрезок из вершины D таким образом, чтобы DE II BC (как это изображено на рисунке 2). Отсюда получаем, что
Пускай DF – будет . Из ΔADE (который будет равнобоким), получим следующее:
Т.е., выражаясь простым языком, мы вначале нашли высоту ΔADE, которая по совместительству является и высотой трапеции. Отсюда вычислим по уже известной формуле площадь четырехугольника ABCD, с уже известным значением высоты DF.
Отсюда, искомая площадь ABCD равна 450 см³. То есть можно с уверенностью сказать, что для того, чтобы вычислить площадь трапеции потребуется только сумма оснований и длина высоты.
Важно!
При решении задача не обязательно найти значение длин по отдельности, вполне допускается, если будут применены и другие параметры фигуры, которые при соответствующем доказательстве будут равны сумме оснований.
Виды трапеций
В зависимости от того, какие стороны имеет фигура, какие углы образованы при основаниях, выделяют три вида четырехугольника: прямоугольная, разнобокая и равнобокая.
Разнобокая
Существует две формы: остроугольная и тупоугольная
. ABCD остроугольна только в том случае, когда углы при основании (AD) острые, а длины сторон разные. Если величина одного угла число Пи/2 более (градусная мера более 90°), то получим тупоугольную.
Если боковины по длине равны
Рисунок 3. Вид равнобокой трапеции
Если непараллельные стороны равны по длине, тогда ABCD называется равнобокой (правильной). При этом у такого четырехугольника градусная мера углов при основании одинакова, их угол будет всегда меньше прямого. Именно по этой причине равнобедренная никогда не делится на остроугольные и тупоугольные. Четырехугольник такой формы имеет свои специфические отличия, к числу которых относят:
- Отрезки соединяющие противоположные вершины равны.
- Острые углы при большем основании составляют 45° (наглядный пример на рисунке 3).
- Если сложить градусные меры противоположных углов, то в сумме они будут давать 180°.

- Вокруг любой правильной трапеции можно построить .
- Если сложить градусную меру противоположных углов, то она равна π.
Более того, в силу своего геометрического расположения точек существуют основные свойства равнобедренной трапеции
:
Значение угла при основании 90°
Перпендикулярность боковой стороны основания — емкая характеристика понятия «прямоугольная трапеция». Двух боковых сторон с углами при основании быть не может,
потому как в противном случае это будет уже прямоугольник. В четырехугольниках такого типа вторая боковая сторона всегда будет образовывать острый угол с большим основанием, а с меньшим — тупой. При этом, перпендикулярная сторона также будет являться и высотой.
Отрезок между серединами боковин
Если соединить середины боковых сторон, и полученный отрезок будет параллельный основаниям, и равен по длине половине их суммы, то образованная прямая будет средней линией.
Значение этого расстояния вычисляется по формуле:
Для более наглядного примера рассмотрим задачу с применением средней линии.
Задача. Средняя линия трапеции равна 7 см, известно, что одна из сторон больше другой на 4 см (рис.4). Найти длины оснований.
Рисунок 4. Решение задачи на поиск длин оснований
Решение. Пусть меньшее основание DC будет равно x см, тогда большее основание будет равняться соответственно (x+4) см. Отсюда, используя формулу средней линии трапеции получим:
Получается, что меньшее основание DC равно 5 см, а большее равняется 9 см.
Важно!
Понятие средней линии является ключевым при решении многих задач по геометрии. На основании её определения, строятся многие доказательства для других фигур. Используя понятие на практике, возможно более рациональное решение и поиск необходимой величины.
Определение высоты, и способы как её найти
Как уже отмечалось ранее, высота представляет собой отрезок, который пересекает основания под углом 2Пи/4 и является кратчайшим расстоянием между ними. Перед тем как найти высоту трапеции,
следует определиться какие даны входные значения. Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Для лучшего понимания рассмотрим задачу. Найти высоту трапеции при условии, что основания равны 8 и 28 см, боковые стороны 12 и 16 см соответственно.
Рисунок 5. Решение задачи на поиск высоты трапеции
Проведем отрезки DF и CH под прямыми углами к основанию AD.Согласно определению, каждый из них будет являться высотой заданной трапеции (рис.5). В таком случае, зная длину каждой боковины, при помощи теоремы Пифагора, найдем чему равна высота в треугольниках AFD и BHC.
Сумма отрезков AF и HB равна разности оснований, т.е.:
Пускай длина AF будет равняться x cм, тогда длина отрезка HB= (20 – x)см. Как было установлено, DF=CH , отсюда .
Тогда получим следующее уравнение:
Получается, что отрезок AF в треугольнике AFD равен 7,2 см, отсюда вычислим по той же теореме Пифагора высоту трапеции DF:
Т.е. высота трапеции ADCB будет равна 9,6 см. Как можно убедиться, что вычисление высоты — процесс больше механический, и основывается на вычислениях сторон и углов треугольников.
Но, в ряде задач по геометрии, могут быть известны только градусы углов, в таком случае вычисления будут производиться через соотношение сторон внутренних треугольников.
Важно!
В сущности трапецию часто рассматривают как два треугольника, или как комбинацию прямоугольника и треугольника. Для решения 90% всех задач, встречаемых в школьных учебниках, свойства и признаки этих фигур. Большинство формул, для этого ГМТ, выведены полагаясь на «механизмы» для указанных двух типов фигур.
Как быстро вычислить длину основания
Перед тем, как найти основание трапеции необходимо определить какие параметры уже даны, и как их рационально использовать. Практическим подходом является извлечение длины неизвестного основания из формулы средней линии. Для более ясного восприятия картинки покажем на примере задачи, как это можно сделать. Пускай известно, что средняя линия трапеции составляет 7 см, а одно из оснований 10 см. Найти длину второй основы.
Решение: Зная, что средняя линия равна половине суммы основ, можно утверждать, что их сумма равна 14 см.
(14 см = 7 см × 2). Из условия задачи, мы знаем, что одно из равно 10 см, отсюда меньшая сторона трапеции будет равна 4 см (4 см = 14 – 10).
Более того, для более комфортного решения задач подобного плана, рекомендуем хорошо выучить такие формулы из области трапеции как
:
- средняя линия;
- площадь;
- высота;
- диагонали.
Зная суть (именно суть) этих вычислений можно без особого труда узнать искомое значение.
Видео: трапеция и ее свойства
Видео: особенности трапеции
Вывод
Из рассмотренных примеров задач можно сделать нехитрый вывод, что трапеция, в плане вычисления задач, является одной из простейших фигур геометрии. Для успешного решения задач прежде всего не стоит определиться с тем, какая информация известна об описываем объекте, в каких формулах их можно применить, и определиться с тем, что требуется найти. Выполняя этот простой алгоритм, ни одна задача с применением этой геометрической фигуры не составит усилий.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.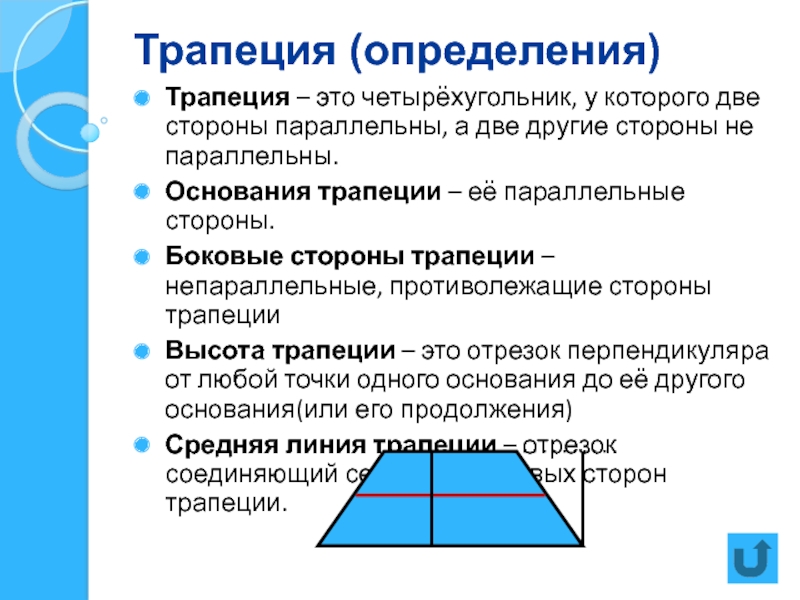
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2
. - Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей.
 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ
. - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b)
.
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2
. - Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2
.
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.

- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2
. - Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2
. Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2
.
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ
. - Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника.
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
. Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников. - Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ
.
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2
. - У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ
. - Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.

- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab
. - И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны.
 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
) не только через высоту, но и через боковую сторону, прилежащую к прямому углу. - Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной
:
- Для начала проведем прямую МХ – МХ || КЕ.
 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение:
Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 .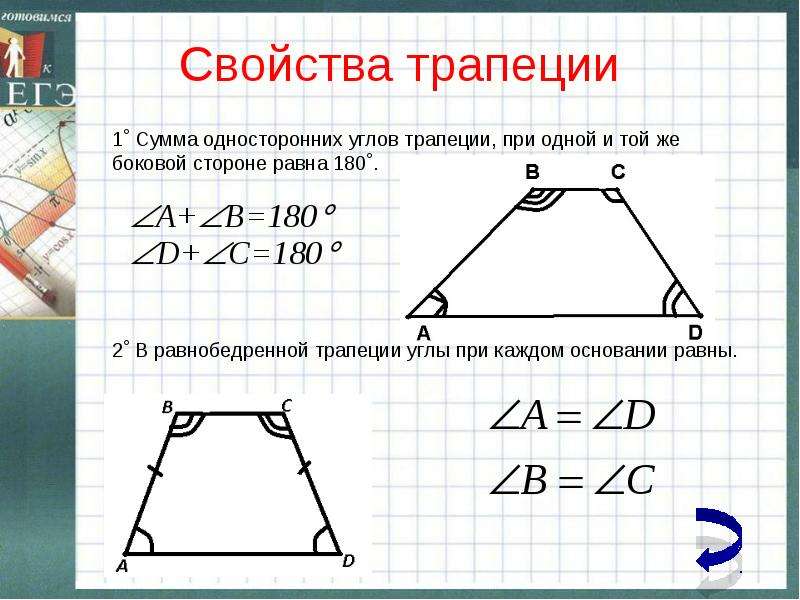 Поэтому КН = ½АВ = 4 см.
Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Трапеция
— это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая
или равнобочная
.
— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b
— основания трапеции
(a
параллельно b
),
m, n
— боковые стороны
трапеции,
d 1 , d 2
— диагонали
трапеции,
h
— высота
трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN
— средняя линия
(отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b
и высоту h
: S = \frac{a + b}{2}\cdot h - Через среднюю линию MN
и высоту h
: S = MN\cdot h - Через диагонали d 1 , d 2
и угол (\sin \varphi
) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия
параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции
, прилежащих к каждой боковой стороне, равна 180^{\circ}
:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими
, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами. {2}
{2}
.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Нахождение площади трапеции
С такими геометрическими фигурами, как трапеции, все мы очень часто встречаемся в жизни. Чаще других с ними приходится иметь дело инженерам-проектировщикам, разрабатывающим различные детали. При этом им практически всегда нужно определять площадь трапеции, форму которой будет иметь то или иное изделие.
На мебельных предприятиях часто изготавливаются столы с трапецеидальными столешницами, которые отличаются не только оригинальным дизайном, но еще и очень удобны в небольших и стесненных помещениях. Для того чтобы точно рассчитать расход материала, требуемого для изготовления этих изделий, их разработчики всегда используют формулу, по которой производится нахождение площади трапеции.
Вычисление площади трапеции
Формула расчёта площади трапеции
a – нижнее основание
b – верхнее основание
h – высота трапеции
S – площадь
Многие современные здания (причем как в городах, так и за их пределами) проектируются таким образом, чтобы их окна имели нестандартную и запоминающуюся форму, в том числе и трапецеидальную. Само собой разумеется, что при их разработке для тех, кто будет их, в конечном итоге, изготавливать, нужно точно определить не только длину нижнего и верхнего основания, а также размеры всех углов, и площадь самой сборки. При этом также применяется формула, на основании которой происходит нахождение площади трапеции. Она, помимо общего расхода материала, необходимого для застекления таких окон, позволяет определить, соответствие в каждом конкретном случае действующим нормам относительно освещенности тех помещений, где их планируется смонтировать.
Детали трапецеидальной формы наличествуют практически в каждом современном автомобиле. К ним, к примеру, относятся почти все стекла, устанавливаемые в дверях. Поэтому при конструировании машин специалистам приходится пользоваться формулами, по которым происходит вычисление площади трапеции.
В последние годы многие наши соотечественники обзаводятся загородными домами, коттеджами и дачами, причем многие из этих строений имеют так называемые вальмовые крыши. Они представляют собой кровельные конструкции, состоящие из четырех скатов, два из которых, являющиеся торцевыми, имеют фору треугольников, а два других – трапеций. На таких крышах практически никогда не задерживается снег, что очень важно в российских условиях. Перед тем, как производить кровельные работы, необходимо определить, какое количество материала для этого потребуется, а это значит, что нужно производить вычисление площади трапеции.
Отправляясь на какой-нибудь морской курорт, где отдыхающие не только проводят время на пляжах, но еще и активно занимаются водными видами спорта, то неподалеку о берега можно увидеть небольшие яхты, некоторые паруса которых изготовлены в форме трапеций.
Тейпирование трапециевидной мышцы
«Грамотное тейпирование трапециевидной мышцы помогает пережить трудный момент с минимальными потерями. Эластичные ленты стабилизируют сегмент опорно-двигательного аппарата с нарушенными функциями — способствуют снижению отечности, восстановлению кровотока и циркуляции лимфы».
Опубликован: 08.04.2021
Обзор материалов из открытых источников.
Автор: исполнительный директор проекта «Травматология и фармакология: точки соприкосновения» Непорожний А. А.
Небольшое отступление. Так как тейпирование очень молодой способ реабилитации, оно бурно развивается. Каждый год-два создаются новые ответвления и даже школы, которые в процессе практики разрабатывают свои, непохожие на классические методы тейпирования от Кензо Касе (Kenzo Kase), способы и методы тейпирования. Данный материал посвящен как раз обзору таких методов. Зачастую, чтобы облегчить состояние пациента, не важно какой метод используется – классическое кинезиотейпирование, биомеханическое или динамическое – главное облегчить страдания пациента.
В верхней части спины и плечевого пояса сконцентрированы жизненно-важные мышцы, даже самые незначительные повреждения и заболевания которых вызывают дискомфорт, нарушают привычный образ жизни и снижают трудоспособность.
Одна из них – Трапециевидная (musculus trapezius). Плоская широкая мышца, занимающая поверхностное положение в задней области шеи и в верхнем отделе спины. Трапециевидная мышца имеет форму треугольника, основанием обращённого к позвоночному столбу, а вершиной — к акромиону лопатки. Трапециевидные мышцы обеих сторон спины вместе имеют форму трапеции.
Функции трапециевидной мышцы
Верхняя часть: При фиксированных позвоночнике и голове поднимает лопатку. При фиксированной лопатке разгибает голову и шею.
Средняя часть: При фиксированных позвоночнике и голове приводит лопатку к позвоночнику. При сокращении всех частей мышцы также происходит приведение лопаток.
Нижняя часть: При фиксированных позвоночнике и голове опускает плечевой пояс.
Главная задача трапециевидной мышцы – управление лопатками: вращение, сведение вместе к позвоночнику. По развитию данных мышцы можно отличить человека, который занимается силовыми видами спорта от легкоатлетов, у них нет такой массивной шеи и рельефной спины.
(подробнее с анатомией трапециевидной мышцы можно ознакомиться в обзорном видео перейдя по ссылке — https://www.youtube.com/watch?v=c_eD5SNDbZs)
Именно трапециевидная мышца, почти всегда задействована, когда мы делаем что-либо руками и именно она устает чаще всего. «Усталость трапеции» очень часто вызывает головные боли, снижает внимание и концентрацию, вызывает онемение в руках и хроническую усталость. Особенно это касается людей, ведущих сидячий образ жизни и много работающих за компьютером (за столом). Тейпирование трапециевидной мышцы необходимо почти всем офисным работникам для снятия напряжения с шеи, верхней части спины и плечевого пояса.
Проблемы с трапецией выбивают из привычного образа жизни, обычная прогулка по городу или отдых на природе причиняют дискомфорт, занятия спортом становятся невозможны и даже малейший поворот головы и попытка поднять руку отзываются мощным спазмом.
Обращение к врачу обязательно закончится назначением лекарственных препаратов, массажа, гимнастики, физиотерапии, иногда уколов (блокад) в места выраженных болевых ощущений.
В арсенале реабилитологов с недавних пор появилось еще одно оружие, помогающее победить проблему – эластичные ленты – тейпы (о истории их создания и принципах работы мы рассказывали в обзорном материале — Кинезиологическое тейпирование).
НО! Стоит помнить — Применение тейпирования трапециевидной мышцы для повышения эффективности работы в сидячем положении это не панацея. Без занятий спортом и специальных упражнений проблемы с трапециевидной мышцей будут нарастать и тогда тейпирование уже не поможет.
Причины появления болей в трапециевидной мышце
Существует распространенное мнение, что для травмирования трапеции (как и любой другой мышцы) нужна активность и нагрузка. Но, в данном случае, мышцы так же страдают из-за пассивности — сидение за компьютером с опущенной головой, долгие поездки в переполненном транспорте или за рулем автомобиля в вынужденном положении.
Рассмотрим основные причины появления патологии:
- Разрывы мышечных волокон. Если постоянно перенапрягаться, будь то жим штанги или марафонский забег, в мышечных волокнах образуются микроразрывы и гематомы.
- Растяжения. Случаются на тренировке, если начать активные упражнения без разминки. Другие факторы риска: подъем тяжестей, резкие движения в которых задействована мышца.
- Ушибы. Следствия механической травмы при занятиях коллективными видами спорта (футболом, баскетболом и хоккеем), падения.
- Хронические заболевания. Тендиниты, артрозы, артриты, капсулиты. Недуги действуют исподтишка, постепенно нарушая функции как отдельных сегментов, так и организма в целом.
- Переохлаждения. От постоянного воздействия низких температур возникают спазмы, а следом появляется миозит – воспаление.
Чтобы симптомы патологии не зашли слишком далеко, можно выполнить тейпирование поврежденной трапециевидной мышцы. Процедура не сотворит чуда, но значительно облегчит болевой синдром и сократит действие травмирующего фактора. А это любое движение.
Диагностика травм и заболеваний трапециевидной мышцы:
Точный диагноз способен поставить только специалист – ортопед-травматолог или хирург. Самостоятельные попытки определить заболевание и заняться самолечением редко приводят к успеху. Но все же есть ряд признаков, которые с высокой доли вероятности, указывают на травмы трапеции:
- Тянущая, ноющая боль в районе мышечного треугольника трапеции – от основания шеи до средней части спины, которая появилась после нагрузки или травмы.
- Спазмы при изменении положения лопаток. Достаточно приподнять вверх плечо, чтобы почувствовать дискомфорт.
- Напряженность мышц. Шея, область верхнего отдела позвоночника и плечевого пояса всегда «в тонусе».
- Скованность движений. Даже обычная ходьба вызывает приступ острой или тянущей боли.
- Гематома (синяк) и отечность в месте травмы.
Понятно, что где лопатки, там и плечевой пояс, и руки. Растяжение, разрыв связок открывают дорогу к длительному восстановлению. Но тейпирование трапециевидной мышцы может сократить этот тоскливый период вплоть до 40 %.
Грамотное тейпирование трапециевидной мышцы помогает пережить трудный момент с минимальными потерями. Эластичные ленты стабилизируют сегмент опорно-двигательного аппарата с нарушенными функциями — способствуют снижению отечности, восстановлению кровотока и циркуляции лимфы.
Так как тема нашего обзора – тейпирование трапециевидной мышцы, мы не будем подробно останавливаться на функциях, заболеваниях и травмах данной области, а сразу перейдем к практике.
Тейпирование трапеции помогает облегчить симптомы следующих патологий:
- Болевые синдромы в верхней части спины и плечевом пояса.
- Артрозы, артриты и другие заболевания плечевого пояса.
- Последствия перегрузок на тренировках.
- Изменения в верхнем отделе позвоночника, возникшие из-за сидячей работы.
Типичная схема тейпирования трапециевидной мышцы
Для начала следует подготовить один прямой пластырь длиной от 20 до 25 сантиметров. До наложения аппликации необходимо определить, в каком положении мышцы боль достигает максимальных значений. Существует 2 варианта:
1. В растянутом состоянии. При наклоне головы влево начинается спазм в правом плече и наоборот. Максимально прижимаем голову к больному плечу. Один якорь ленты клеим на верхнюю часть лопатки, второй – на основание черепа без натяжения. Получится «мостик», который останется разгладить.
2. В сжатом состоянии. Неприятные ощущения начинаются при движении шеи к очагу патологии. Отводим голову в противоположную сторону от больного места. Накладываем тейп с натяжением 10 % от плеча к шее.
Подробнее с процессом тейпирования можно ознакомиться, посмотрев видео по ссылке https://www.youtube.com/watch?v=yVlYtCPrKCw)
Другой вариант – тейпирование трапециевидной мышцы лентой в форме буквы Y (принцип фиксации как в первом варианте).
Сначала наклеивается тейп по верхней части трапеции, а затем по средней.
И еще один вариант тейпирования трапециевидной мышцы с более жесткой фиксацией
Выбор тейпов для тейпирования трапециевидной мышцы
На рынке полно контрафакта. Поэтому покупать материалы нужно в проверенных местах, а лучше всего напрямую от производителей в фирменных магазинах. Это даст хоть какие-то гарантии, хотя от поставок бракованной продукции не застрахованы даже крупные специализированные магазины и аптеки.
Типичный набор признаков подделки:
1. Низкое качество полиграфии на упаковке. Буквы прочитать сложно, дизайн явно готовил дилетант. Тусклые цвета, ошибки в словах.
2. Едкий химический запах. В составе подлинных тейпов минимум вредных компонентов. Основа – хлопок или нейлон, для фиксации – клеящий состав.
3. Надпись — «Сделано в КНР». Хотя китайские производители улучшают качество продукции, лучшие образцы все еще поступают в продажу в магазины только из Южной Кореи.
Советы по работе с эластичными лентами
Для начала нужно определиться с шириной ленты. Для трапеции подойдут полосы с общей шириной от 5 сантиметров. Более узкие не способны дать нужного эффекта. Перед накладыванием аппликации следует подготовить кожу. От этого зависит уровень комфорта и срок ношения тейпа:
- Протираем поверхность салфеткой, пропитанной спиртом.
- Удаляем волоски (следует помнить, что верхняя часть ленты-тейпа не наклеивается на волосистую часть головы).
Следующая цель – подготовить пластыри к наклейке. Для этого отмеряют отрезок нужной длины и отрезают. Угловатые края могут зацепиться за одежду или экипировку, а значит, их следует закруглить. Подойдут обычные острые ножницы.
Нельзя сразу отклеивать подложку полностью, есть риск случайно прикоснуться к липкому слою. Это снизит силу фиксации и продолжительность ношения.
Когда процедура тейпирования будет завершена, останется лишь растереть полосы энергичными движениями. Это активирует липкий слой и удалит пузырьки воздуха, оставшиеся под лентой. Тейп начнет действовать. Воспалительный процесс сократится, а мышца, благодаря разгрузке, восстановится быстрее.
Еще раз хотим напомнить об опасности самолечения и самодиагностики. Сэкономив время и деньги на посещении и консультации специалистов ортопедов-травматологов, хирургов или реабилитологов, вы рискуете перевести острый процесс, который можно быстро вылечить с минимальными потерями, в хронический, на лечение которого уйдет масса времени и средств!
Один из лучших специалистов по тейпированию в Киеве и Украине, наш хороший друг и участник проекта, реабилитолог, специалист кинезиологического и биомеханического тейпирования, физической реабилитации Андрей Кифа. Записаться к нему на консультацию можно по E-mail:[email protected] или по телефону +380679082493
Берегите себя, доверяйте специалистам и будьте здоровы!
Другие материалы
Пяточная шпора (плантарный фасциит)Актуальные вопросы артроскопической хирургии акромиально-ключичного сустава
| ФГКОУ «МКК «Пансион воспитанниц МО РФ» «УТВЕРЖДАЮ» Руководитель отдельной дисциплины (математика, информатика и ИКТ) Ю. В. Крылова _____________ «___» _____________ 2015 г. «Трапеция и ее свойства» Методическая разработка преподавателя математики Шаталиной Елены Дмитриевны
Москва 2015 год Оглавление Введение 2
. 10. Заключение . Список используемой литературы Приложение
Введение Данная работа посвящена геометрической фигуре, которая называется трапеция. «Обычная фигура»,- скажете вы, но это не так. Она таит в себе много тайн и загадок, если приглядеться и углубиться в ее изучение, то вы откроете для себя много нового в мире геометрии, задачи, которые раньше не решались, покажутся вам легкими. Трапеция — греч.слово trapezion – «столик». Заимств. в 18 в. из лат. яз., где trapezion – греч. Это четырехугольник, у которого две противоположные стороны параллельны. Трапеция встречается впервые у древнегреческого ученого Посидония (2 век до н.э.). В нашей жизни много разных фигур. В 7 классе мы близко познакомились с треугольником, в 8 классе по школьной программе мы начали изучать трапецию. Эта фигура заинтересовала нас, а в учебнике непозволимо мало про нее написано. Поэтому мы решили взять это дело в руки и найти информацию про трапецию. ее свойства. В работе рассматриваются свойства знакомые воспитанницам по пройденному материалу в учебнике, но в большей степени неизвестные свойства, которые необходимы для решения сложных задач. Чем больше количество решаемых задач, тем больше вопросов возникает при решении их. Ответом на эти вопросы иногда кажется тайной, узнавая, новые свойства трапеции, необычные приемы решения задач, а также технику дополнительных построений, мы постепенно открываем тайны трапеции. В интернете, если забить в поисковике, о методах решения задач по теме «трапеция» очень мало литературы. В процессе работы над проектом найден большой объем информации, которая поможет воспитанницам в глубоком изучении геометрии. Трапеция.
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны. Если боковые стороны равны, трапеция называется равнобедренной. Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции. Расстояние между основаниями называется высотой трапеции. 2. Свойства равнобедренной трапеции
3. Диагонали равнобедренной трапеции равны. 4. Высота равнобедренной трапеции, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
10. Проекция боковой стороны равнобедренной трапеции на большее основание равна полуразности оснований, а проекция диагонали равна помусумме оснований.
Если сумма оснований трапеции равна сумме боковых сторон, то в неё можно вписать окружность. Е 4. Свойства вписанных и описанных трапеций
2.Если в равнобедренную трапецию можно вписать окружность, то сумма длин оснований равна сумме длин боковых сторон. Следовательно, длина боковой стороны равна длине средней линии трапеции. 4. Если в трапецию вписана окружность, то боковые стороны из ее центра видны под углом 90°.
1 5. Средние величины в трапеции Среднее геометрическое
1. Середины диагоналей трапеции и середины боковых сторон лежат на одной прямой. 2. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 3. Отрезки прямой, параллельной основаниям трапеции, пересекающей боковые стороны и диагонали трапеции, заключенные между боковой стороной диагональю, равны.
5. При пересечении диагоналей произвольной трапеции образуются четыре треугольника с общей вершиной, причем треугольники, прилежащие к основаниям, подобны, а треугольники, прилежащие к боковым сторонам, равновелики(т.е. имеют равные площади). 6.Сумма квадратов диагоналей произвольной трапеции равна сумме квадратов боковых сторон, сложенной с удвоенным произведением оснований.
7 8. Прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки. 9. Отрезок, параллельный основаниям и проходящий через точку пересечения диагоналей, делится последней пополам. 7. Признаки трапеции
8. Дополнительные построения в трапеции 1. Отрезок, соединяющий середины боковых сторон — средняя линия трапеции. 3. Если даны все стороны трапеции, через вершину меньшего основания проводится прямая, параллельная боковой стороне. Получается треугольник со сторонами, равными боковым сторонам трапеции и разности оснований. По формуле Герона находят площадь треугольника, потом высоту треугольника, которая равна высоте трапеции. 5. Высоты трапеции, опущенные из вершин одного основания, высекают на прямой, содержащей другое основание, отрезок, равный первому основанию. 6 7.Отрезок, соединяющий середины диагоналей, равен полуразности оснований трапеции. 8. Биссектрисы углов, прилежащих к одной из боковых сторон трапеции, они перпендикулярны и пересекаются в точке, лежащей на средней линии трапеции, т.е., при их пересечении образуется прямоугольный треугольник с гипотенузой, равной боковой стороне. 9. Биссектриса угла трапеции отсекает равнобедренный треугольник. 1 12. Продолжение боковых сторон трапеции до пересечения дает возможность рассматривать подобные треугольники. 9. Площадь трапеции 1. Площадь трапеции равна произведению полусуммы оснований на высоту S = ½(a + b)•h или П 2. Площадь трапеции равна произведению боковой стороны и перпендикуляра, проведенного из середины другой боковой стороны к прямой, содержащей первую боковую сторону.
10. Заключение ГДЕ, КАК И ДЛЯ ЧЕГО ИСПОЛЬЗЕУТСЯ ТРАПЕЦИЯ? Трапеция в спорте: Трапеция — безусловно прогрессивное изобретение человечества. Она предназначена для того, чтобы разгрузить наши руки, сделать хождение на виндсерфере комфортным и легким отдыхом. Хождение на короткой доске вообще не имеет смысла без трапеции, так как без нее невозможно правильно распределить тягу между степсом и ногами и эффективно разогнаться. Трапеция в моде: Трапеция в одежде была популярна ещё в средние века, в романскую эпоху IX-XI вв. В тот период основу женской одежды составляли туники в пол, к низу туника сильно расширялась, что и создавало эффект трапеции. Возрождение силуэта произошло в 1961-ом году и стало гимном молодости, независимости и утонченности. Огромную роль в популяризации трапеции сыграла хрупкая модель Лесли Хорнби, известная, как Твигги. Невысокая девочка с анорексичным телосложением и огромными глазами стала символом эпохи, а её излюбленными нарядами были короткие платья трапеции. Трапеция в природе: трапеция встречается и в природе. У человека есть трапециевидная мышца, у некоторых людей лицо имеет форму трапеции. Лепестки цветов, созвездия, и конечно же вулкан Килиманджаро тоже имеют форму трапеции. Трапеция в быту: Трапеция используется и в быту, т.к ее форма практична. Она встречается в таких предметах как: ковш экскаватора, стол, винт, машина. Трапеция — символ архитектуры инков. Доминирующая стилистическая форма в архитектуре инков проста, но изящна — это трапеция. Она имеет не только функциональное значение, но и строго ограниченное художественное оформление. Трапециевидные дверные проемы, окна, и стенные ниши найдены в постройках всех типов, и в храмах и в менее значительных зданиях более грубых, если можно так выразиться, постройках. Трапеция встречается и в современной архитектуре. Эта форма зданий является необычной, поэтому такие постройки всегда притягивают взгляды прохожих. В 21 первом веке люди уже практически не задумываются о значении геометрических фигур в их жизни. Их совершенно не волнует какой формы у них стол, очки или телефон. Они просто выбирают ту форму, которая практична. Но именно от формы той или иной вещи может зависеть использование предмета, его предназначение, результат работы. Сегодня мы познакомили вас с одной из величайших достижений человечества- с трапецией. Мы приоткрыли вам дверь в удивительный мир фигур, поведали вам тайны трапеции и показали, что геометрия вокруг нас. Список используемой литературы
Приложение 1.Доказательство некоторых свойств трапеции. 1. Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках K и L. Доказать, что если основания трапеции равны а и b, то длина отрезка KL равна среднему геометрическому оснований трапеции. Доказательство Пусть О — точка пересечения диагоналей, AD = а, ВС = b. Прямая KL параллельна основанию AD, следовательно, KО║ AD, треугольники ВKО и BAD подобны, поэтому
( 2 ) Подставим ( 2 ) в ( 1 ), получим KO = Аналогично LO = Тогда K L= KO + LO =
Д Обозначим ВМ = х, МС = у, AN = и, ND = v. Имеем: ∆ВКМ ~ ∆AKN → x B C Y O v u N D ∆CMO ∆ANO поэтому . Перемножая полученные равенства, получим , откуда следует x=y, но тогда и u = v.
3. Задачи по теме «Трапеция» повышенной сложности. Садовничий Ю.В. «Математика. Подготовка к ЕГЭ», Москва, ИЛЕКСА, 2011, стр. 252. 1 . В трапеции диагонали равны 3 и 5, а отрезок, соединяющий середины оснований, равен 2. Найти площадь трапеции. Ответ: S = 6. 2. Периметр равнобочной трапеции, описанной около круга, равен р. Найти радиус этого круга, если известно, что острый угол при основании трапеции равен ɑ. psina Ответ: 1и 7.
Ответ: S= 3ab В трапеции PQRS длина основания QR равна 10, длина диагонали QS равна 19, а величина угла QSP равна 30°. Выяснить, что больше, длина основания QR или длина стороны RS. Ответ: RS > QR.
Ответ: S=90√3. Иванов А.А., Иванов А.П., Математика: Пособие для подготовки к ЕГЭ и поступлению в вузы. – М.: Издательство МФТИ, 2003, стр. 238.. 12. Площадь прямоугольной трапеции равна S, острый угол равен а. Найти высоту трапеции, если ее меньшая диагональ равна большему оснозанию. [√2Sctg а]
[arccos(l — 1/к), π — arccos(l — 1/к), к > 1]
[√Stg(½ ɑ)]
4. Проверочный тест по теме «Трапеция» В трапеции, имеющей прямой угол, основания равны 5 и 11, а большая диагональ √185. Площадь трапеции составляет В трапеции боковые стороны и меньшее основание равны Ь, а острый угол вдвое меньше тупого. Площадь трапеции равна 151 в равнобедренной трапеции, описанной около окружности радиуса 5 м и имеющей основание 20 м, другое основание равно Меньшее основание трапеции, вписанной в окружность, втрое меньше большего, которое является диаметром окружности.25j В трапеции с диагональю 20, высотой 12 и площадью 150 вторая диагональ равна 29j Равнобедренная трапеция с острым углом а описана около окруж- ности. Отношение ее большего основания к меньшему равно Зо| В описанной около круга равнобочной трапеции расстояние от центра круга до дальней вершины трапеции втрое больше, чем до ближней. Тангенс острого угла трапецииравен Достарыңызбен бөлісу: |
Распределения продолжительности жизни и таблицы смертности
Введение
Вероятности, относящиеся к возрасту в момент смерти
Функция дожития
Продолжительность предстоящей жизни для лица в возрасте х
Пошаговая продолжительность предстоящей жизни
Интенсивность смертности
Таблицы смертности
Связь функций, содержащихся в таблице смертности, с функцией дожития
Пример таблицы смертности
Другие характеристики, связанные с таблицами смертности
Селекционные и заключительные таблицы
Введение
Страхование может увеличить ожидаемую полезность для лица, подвергающегося риску случайных потерь. Основой простых моделей для страховых договоров, заключенных на один временной период, являются бернуллиевские случайные величины, отражающие наступление или ненаступление страхового случая.
Наступление страхового случая в некоторых примерах приводит к другому случайному процессу, определяющему величину потерь. Существуют модели страховых систем, предназначенных для работы со случайными потерями, в которых случайность связана с тем, насколько долго будет жить некое лицо.
Основным структурным элементом подобных моделей является случайная величина, называемая продолжительностью предстоящей жизни (временем дожития) и обозначаемая через Т(х).
Итак, изложим ряд идей, которые позволят описывать и использовать распределение как этой случайной величины, так и соответствующего ей возраста в момент смерти Х.
Покажем, как распределение случайной величины «возраст в момент смерти» можно представить посредством таблицы смертности. Эти таблицы полезны во многих областях знания. Поэтому в каждой из этих разнообразных областей, где используются таблицы смертности, была разработана свои терминология и обозначения.
Например, инженеры используют таблицы смертности для изучения надежности сложных механических и электронных систем.
В биостатистике таблицы смертности используются для сравнения эффективности различных методов лечения серьёзных заболеваний.
Демографы используют таблицы смертности как средство популяционного проектирования. Мы будем использовать таблицы смертности для построения моделей страховых систем, призванных содействовать людям, находящимся перед лицом неопределенности, связанной с моментом наступления их смерти.
Таблица смертности является незаменимой компонентой многих моделей актуарной науки. Некоторые исследователи считают датой рождения актуарной науки 1693 год. В этом году Эдмунд Галлей (E. Halley) опубликовал труд «An Estimate of the Degrees of the Mortality of Mankind, Drawn from Various of Births and Funerals at the City of Breslau» («Оценка степени смертности человечества, выведенная из различных таблиц рождения и погребения в городе Бреславле»).
Таблицы смертности, названные Бреславльскими, которые содержатся в статье Галлея, по-прежнему представляют интерес из-за удивительно современной системы обозначений и понятий.
Вероятности, относящиеся к возрасту в момент смерти
Опишем неопределенность, связанную с возрастом в момент наступления смерти, в вероятностных терминах.
Функция дожития
Рассмотрим новорожденного. Возраст в момент смерти Х для этого новорожденного является случайной величиной непрерывного типа. Обозначим через функцию распределения этой случайной величины,
и положим
Мы будем всегда предполагать, что , откуда следует, что s(0)=1.
Функция s(x) называется функцией дожития. Для любого положительного х величина s(x) является вероятностью того, что новорожденный достигнет возраста х. Распределение с.в. Х может определяться либо заданием функции распределения либо функции s(x).
В актуарной науке и в демографии функция дожития традиционно использовалась как исходная точка для дальнейших исследований.
В теории вероятностей и в статистике такую роль играет функция распределения. Однако из свойств функции распределения мы можем вывести соответствующие свойства функции дожития.
Опираясь на вероятностные законы, мы можем формулировать вероятностные утверждения о возрасте в момент смерти в терминах либо функции дожития, либо функции распределения.
Например, вероятность того, что новорожденный умрет в возрасте между х и z(x<z), равна
Продолжительность предстоящей жизни для лица в возрасте х
Условная вероятность того, что новорожденный умрет в возрасте между х и z при условии, что он доживет до возраста х, равна
(2.3)
Символ (х) используется для обозначения лица возраста х. Продолжительность предстоящей жизни этого лица (х), Х — х, обозначается через Т(х).
Актуарные символы отличаются от обозначений, принятых в теории вероятностей, и читатель, возможно, с ними не знаком. Например, функция одного переменного, которая записывается в виде q(x) в вероятных обозначениях, в этой системе будет записываться в виде qx.
Аналогично, функция многих переменных записывается в актуарных обозначениях при помощи комбинации верхних и нижних индексов и иных символов.
Для формулировки вероятных утверждений о Т(х) мы будем пользоваться обозначениями
(2.4)
(2.5)
Символ можно интерпретировать как вероятность того, что (х) умрет в течение ближайших t лет. Другими словами, является функцией распределения с.в. Т(х). С другой стороны может интерпретироваться как вероятность того, что (х) достигнет возраста х+t. Другими словами, является функцией дожития для (х). В частном случае лица в возрасте 0 мы имеем Т(0)=Х и
(2.6)
Если t=1 тот по соглашению мы можем опускать первый индекс в обозначениях, введенных формулами (2.4) и (2.5), получая
qx=P[(x) умрет в течение одного года],
px=P[(x)доживет до возраста х+1 лет].
Существует специальный символ для более общего события, состоящего в том, что (х) проживет t лет и умрет в течение последующих u лет, т.е. что (х) умрет в возрасте между x+t и x+t+u, а именно
(2.7)
Как и ранее, если u=1, то соответствующий нижний индекс в обозначении опускается, и мы получаем символ .
Сейчас у нас есть два выражения для вероятности того, что (х) умрет в возрасте между х и x+u. Формула (2.7) при t=0 дает первое из этих выражений, а формула (2.3) с z=x+u — второе выражение. Будут ли эти две вероятности различными?
Формула (2.3) может интерпретироваться как условная вероятность того, что новорожденный умрет в возрасте между х и z=x+u при условии, что он доживет до возраста х.
Единственная информация о новорожденном, к настоящему моменту достигшем возраста х, состоит в том, что он дожил до этого возраста. Поэтому рассматриваемое вероятностное утверждение основано на условном распределении при условии дожития для новорожденных.
С другой стороны, формула (2.7) при t=0 определяет вероятность того, что лицо, наблюдаемое в возрасте х, умрет в возрасте между х и х+u.
Данные о лице в возрасте х могут содержать не только информацию о том, что оно дожило до этого возраста. Это может быть информация о том, что рассматриваемое лицо прошло медицинское обследование перед заключением договора о страховании, или же о том, что это лицо только что начало курс лечения от серьезного заболевания.
Таблицы смертности в том случае, когда данные о лице в возрасте х содержат не только информацию, что новорожденный дожил до возраста х, обсуждаются в разделе 8, где для этих таблиц вводятся дополнительные обозначения.
Будем продолжать развивать теорию, предполагая, что формулы (2.3) и (2.7) не содержат смысловых различий, т.е. будем до раздела 8 считать, что информация о лице, дожившем до возраста х, дает то же условное распределение продолжительности предстоящей жизни, что и информация о дожитии новорожденного до возраста х, а именно
(2.8)
(2.9)
При таком подходе формула (2.7) и многие её частные случаи могут быть выражены в виде
(2.10)
Пошаговая продолжительность предстоящей жизни
С продолжительностью предстоящей жизни связана дискретная случайная величина, определяющая число полных будущих лет, прожитых лицом (х) до смерти. Она называется пошаговой продолжительностью предстоящей жизни лица (х) и обозначается через К(х). Поскольку с.в. К(х) является наибольшим целым числом, не превосходящим Т(х), ее функция вероятностей задается выражением
k=0,1,2,… (2.11)
Перемена неравенств местами здесь возможна, поскольку при наших предположениях о том, что распределение Т(х) непрерывно, Р[Т(х)=k]=P[T(x)=k+1]=0. Формула (2.11) является частным случаем формулы (2.7), где u=1 и k является неотрицательным целым числом. Из соотношения (2.11) следует, что функция распределения с.в. К(х) является ступенчатой функцией и
и k является целой частью числа у.
Часто из контекста ясно, что Т(х) является продолжительностью предстоящей жизни лица (х). В этом случае мы будем писать Т вместо Т(х). Аналогично, мы будем писать К вместо К(х).
Интенсивность смертности
Формула (2.3) выражает в терминах функции распределения и в терминах функции дожития условную вероятность того, что лицо (0) умрет в возрасте между х и z при условии, при условии, что оно доживет до возраста х.
Если разность z-x постоянна и равна, скажем с, то рассматриваемая как функция от х, эта условная вероятность описывает распределение вероятности смерти в ближайшем будущем (между моментами времени 0 и с) для лица, достигшего возраста х. Аналог этой функции, рассматривающий смерть в определенный момент, можно получить, используя плотность вероятности смерти по достижении возраста х, т.е. формулу (2.3) с ,
,(2.12)
В этом выражении является функцией плотности непрерывной случайной величины «возраст в момент смерти». Функция в формуле (2.12) может интерпретироваться в терминах условных плотностей. Для каждого возраста х она дает значение в точке х условной функции плотности с.в. Х при условии дожития до возраста х и обозначается через .
Мы получаем
(2.13)
Из свойств функций следует, что .
В актуарной науке и в демографии называется интенсивностью смертности. В теории надежности, которая занимается исследованием вероятностей безотказной работы механизмов и систем, эта величина называется интенсивностью отказов.
Как и функция дожития, интенсивность смертности может использоваться для определения распределения с.в.Х. Чтобы это сделать, заменим в формуле (2.13) х на у и после некоторых преобразований получим
Интегрируя это выражение от х до х+n, получим
Потенцируя получаем
(2.14)
Иногда удобно переписать формулу (2.14), сделав замену s=у-х:
(2.15)
В частности, мы изменим обозначения с тем, чтобы они соответствовали использованным в формуле (2.6), положив возраст уже живших лиц равным 0 и обозначив возраст дожития через х. Тогда мы получим
(2.16)
Кроме того,
(2.17)
и (2.18)
Пусть обозначает соответственно функцию распределения и функцию плотности с.в. Т(х), продолжительности предстоящей жизни лица (х). Заметим, что (см. обозначения (2.4)). Таким образом,
(2.19)
Значит, является вероятностью того, что лицо (х) умрет в возрасте между t и t+dt, и
где в качестве верхнего предела интегрирования записано «плюс бесконечность» (это сокращенная запись интегрирования по всей области изменения функции плотности, лежащей на положительной полуоси).
Из формулы (2.19) следует, что
(2.20)
Эта эквивалентная форма бывает полезной в некоторых рассуждениях актуарной математики.
Поскольку мы имеем . Таким образом
В нижней половине таблицы 2.1. собраны некоторые соотношения между стандартными функциями теории вероятностей и функциями, характерными для приложений, связанных с возрастом в момент смерти.
Можно привести много примеров, когда соотношения, связанные с возрастом в момент смерти, можно переформулировать в более общих вероятностных терминах. Следующий пример это иллюстрирует.
Пример 2.1. Если обозначает дополнение события А в некотором выборочном пространстве и если , то следующее соотношение является вероятностным тождеством
Перепишем это тождество в актуарных обозначениях для событий
.
Решение. Вероятность переписывается в виде превращается в
Таким образом, мы получаем
Таблица 2.1. Некоторые функции для с.в. Х, возраста в момент смерти
Таблицы смертности
Публикуемая таблица смертности обычно содержит расположенные по возрастам индивидуумов значения основных функций и, возможно, дополнительных функций, получаемых из них.
Перед тем как представить такую таблицу, рассмотрим интерпретацию таких функций, которая непосредственно связана с вероятностными функциями, обсуждавшимися в разделе 2.
Связь функций, содержащихся в таблице смертности, с функцией дожития
В формуле (2.9) мы выразили условную вероятность того, что лицо (х) умрет в течение t лет, следующим образом:
и, в частности,
Рассмотрим теперь группу из l0 новорожденных, положив, например, l0=100 000. Для каждого новорожденного случайная величина «возраст в момент смерти» имеет распределение, заданное функцией дожития s(x). Будем обозначать через L(x) число лиц в группе, доживших до возраста х. Припишем всем лицам в группе номера j=1,2,3,…,l0 и заметим, что
где является индикатором дожития лица с номером j, т.е.
Так как E[Ij] = s(x), то
Мы обозначим Е[λ(х)] через lx , это означает, что lx — математическое ожидание числа доживших до возраста х из l0 новорожденных, и мы имеем
(3.1)
Далее, в предположении, что индикаторы IJ взаимно независимы, λ(х) имеет биномиальное распределение с параметрами n= l0 и р = s ( x ). Отметим, однако, что в равенстве (3.1) не требуется предположения о независимости.
Аналогично, обозначим через ПDX число умерших в возрасте между х и х + п из начальной совокупности, состоящей из l0 лиц.
Мы обозначаем Е[ПDX] через ПdX .
Поскольку для новорожденного вероятность смерти в возрасте между х и х + п равна s ( x ) — s ( x + n), используя рассуждения, приводившиеся выше относительно lx , получим
(3.2)
Если n = 1, мы опускаем левый нижний индекс в выражениях ПDX и ПdX.
Из формулы (3.1) видно, что
и (3.3)
(3.4)
Поскольку
сомножитель lxμ(х) в (3.4) можно интерпретировать как ожидаемую плотность смертей в возрастном интервале (х,х + dх). Заметим, далее, что
, (3.5)
, (3.6)
(3.7)
Для удобства ссылок мы будем называть группу из l0 новорожденных, каждый из которых имеет функцию дожития s ( x ), совокупностью случайного дожития.
Пример таблицы смертности
В приводимой ниже табл. 3.1, которая называется «Таблица смертности населения: США, 1979-1981», функции tqX ,lx , tdX представлены для l0 = 100000.
За исключением первого года жизни, значение t в табулируемых функциях tqX и tdX равно 1. Другие функции, содержащиеся в этой таблице, рассматриваются в разд. 3.5.
Эта таблица создавалась не на основе наблюдений за 100000 новорожденными вплоть до смерти последнего из них. Она была основана на оценках вероятностей смерти при условии дожития до различных возрастов, полученных из данных о народонаселении США в годы, близкие к 1980-му году, году переписи населения.
Используя понятие совокупности случайного дожития, мы должны сделать предполoжение, что вероятности, полученные на основе этой таблицы, будут соответствовать продолжительности жизни тех, кто принадлежит к этой совокупности дожития.
Полезно сделать ряд замечаний относительно приведенной таблицы.
Замечания.
• Ожидается, что примерно 1% новорожденных, входящих в совокупность дожития, умрет на первом году жизни.
• Следует ожидать, что примерно 77% из группы новорожденных доживет до возраста 65 лет.
• Максимальное число смертей в группе ожидается в возрасте между 83 и 84 годами.
• Известно мало случаев, когда смерть наступает в возрасте свыше 110 лет. Поэтому часто предполагается, что существует такой возраст w , что s ( x ) > 0 для x < w и s ( x ) = 0 для x>= w .
Если существование такого возраста w предполагается, то он называется предельным возрастом . Для приведенной таблицы предельный возраст не определен. Очевидно, имеется положительная вероятность дожить до 110 лет, но таблица не содержит указаний на возраст w .
• Локальные минимумы для ожидаемого числа смертей расположены в районе 11 и 27 лет, а локальный максимум — в районе 24 лет.
• Хотя значения lx были округлены до целых чисел, в соответствии с формулой (3.3.1) делать это не обязательно.
Такое представление информации, как табл. 3.1, является стандартным методом описания распределения возраста в момент смерти.
Другим способом является представление функции дожития в аналитической форме, такой, как s(x)=e-cx , c>0 , x>=0. Однако большинство исследований смертности среди людей для нужд страхования использует представление s ( x ) — l0x / lx , что иллюстрируется табл.3.1.
Поскольку величина 100000s(x) представлена только для целых значений х, при вычислении s(x) для нецелых значений аргумента необходимо прибегать к интерполяции. Этот вопрос обсуждается в разд. 3.6.
Пример 3.1. Используя табл. 3.1, вычислим вероятность того, что лицо (20)
1) доживет до возраста 100,
2) умрет, не доживя до 70 лет,
3) умрет в десятой декаде своей жизни.
Решение.
1)
2)
3)
Чтобы оценить роль таблиц смертности, рассмотрим рис. 3.1, 3.2 и 3.3. Они отражают текущую смертность народонаселения, а не данные, приведенные в табл. 3.1.
На рис. 3.1 надо обратить внимание на следующее:
• интенсивность смертности положительна, и требование , очевидно, выполнено
• интенсивность смертности довольно высока на начальном этапе, а затем резко снижается до минимума в окрестности возраста 10 лет.
На рис. 3.2 и 3.3 надо обратить внимание на следующее:
• функция lxμ(x) пропорциональна функции плотности с.в. «возраст в момент смерти» для новорожденного. Поскольку lxμ(x) является ожидаемой плотностью смертей в возрасте х, когда речь идет о совокупности случайного дожития, график функции lxμ(x) называется кривой смертности.
• функция lxμ(x) имеет локальный минимум в окрестности возраста 10 лет. Мода распределения смертей, т. е. возраст, в котором реализуется максимум кривой смертности, находится в районе 80 лет.
• функция lx пропорциональна функции дожития lxμ(x). Ее также можно интерпретировать как ожидаемое число доживших до возраста х из всей исходной группы, состоявшей из l0 лиц.
• точки локального экстремума функции lxμ(x) соответствуют точкам перегиба функции lx, поскольку
4. Совокупность детерминированного дожития
Перейдем ко второй, невероятностной, интерпретации таблиц смертности. С точки зрения математики она восходит к понятию коэффициента выбытия (отрицательного роста) и потому связана с приложениями к задачам о скорости роста в биологии и в экономике. Она по природе детерминистическая и приводит к понятию совокупности детерминированного дожития, или когорты.
Совокупность детерминированного дожития, как вытекает из таблицы смертности, имеет следующие характеристики:
• изначально она состоит из l0 лиц возраста 0.
• для членов совокупности в любом возрасте действуют фактические годовые коэффициенты смертности (выбытия), которые определяются величинами qx в таблице смертности.
• совокупность является замкнутой. В нее не может входить никто, кроме тех l0 лиц, которые находились в ней в самом начале. Выход из этой совокупности обусловлен фактическими годовыми коэффициентами смертности (выбытия) и только ими.
Из приведенных характеристик вытекает, что
………………………….. (4.1)
где lx обозначает число лиц, доживших до возраста х в совокупности дожития. Эта цепочка равенств, порожденная числом l0, называемым корнем таблицы смертности, и множеством значений qx , может быть переписана в виде
,
,
………….. (4.2)
Между совокупностью детерминированного дожития и моделью сложных процентов имеется аналогия, некоторые положения которой суммируются в табл. 4.1.
Таблица 4.1. Понятия теории сложных процентов и соответствующие им понятия в теории совокупностей детерминированного дожития
|
Сложные проценты
|
Совокупность дожития
|
|---|---|
|
A ( t )=Величина капитала в момент времени t , время измеряется в годах
|
lx =Размер группы возраста x , возраст измеряется в годах
|
|
Эффективная годовая процентная ставка (приращения)
|
Фактический годовой коэффициент смертности (выбытия)
|
|
Эффективная n -летняя процентная ставка, начиная с времени t
|
Фактический –летний коэффициент смертности, начиная с возраста х
|
|
Интенсивность счисления процента в момент времени t
|
Интенсивность смерти в возрасте х
|
Заголовки к столбцам табл. 3.1 для tqx ,lx, tdx относятся к совокупности детерминированного дожития. Хотя математические основы для совокупностей случайного и детерминированного дожития различны, функции tqx ,lx, tdx имеют одинаковые математические свойства и анализируются одинаково.
Понятие совокупности случайного дожития имеет то преимущество, что позволяет пользоваться всем аппаратом теории вероятностей. Совокупность детерминированного дожития концептуально проще и ее легче использовать, но она не отражает случайных колебаний числа доживших до определенного возраста.
Другие характеристики, связанные с таблицами смертности
Выведем выражения для некоторых общеупотребительных характеристик распределений с.в. T(х) и K(х) и введем общий метод вычислений некоторых из этих характеристик.
Характеристики
Математическое ожидание с.в. Т(х), обозначаемое через èx, называется полной ожидаемой продолжительностью жизни. Используя интегрирование по частям, мы получим
(5.1)
Из существования E [T(x)] следует соотношение . Таким образом,
(5.2)
Полная ожидаемая продолжительность жизни в различных возрастах часто используется для сравнения уровней общественного здравоохранения различных стран. Аналогичное интегрирование по частям дает эквивалентное выражение для E [T(x)2] :
(5.3)
Этот результат полезен для вычисления D [ T ( x )] по формуле
(5.4)
Во всех приведенных выкладках мы предполагали, что E [T(x)] и E [T(x)2] существуют. Можно построить функцию дожития s ( x ) = (1 + х) -1 , для которой это будет не так.
Можно определить другие характеристики распределения с.в. Т(х). Медиану продолжительности предстоящей жизни лица (x), которая обозначается через m ( x ) , можно найти как решение уравнения
или
относительно m (х). В частности, m(0) является решением уравнения s [m (0)] = 1/2. Мы также можем найти моду распределения с.в. Т(х), указав значение t , которое доставляет максимальное значение функции tPxμ(x+t) .
Математическое ожидание с.в. К(х) обозначается через еx . Эта величина называется пошаговой ожидаемой продолжительностью жизни. Применяя определение и описанное в приложении 5 суммирование по частям, мы получаем
(5.6)
Снова из существования E [ K ( x )] следует соотношение limkk–> ∞(- kpx )=0 . Таким образом, проведя замену переменной, по которой проводится суммирование, имеем
(5.7)
Повторяя рассуждения, проведенные для непрерывной модели, и пользуясь формулой суммирования по частям, получаем
(5.8)
Из существования Е[ K ( x )2 ] вытекает соотношение limkk–> ∞k2(- kpx )=0 .Проведя замену переменной, по которой производится суммирование, получаем
(5.9)
Далее ,
(5.10)
Для завершения обсуждения некоторых компонент табл. 3.1 мы должны ввести дополнительные функции. Символ L2 обозначает общее ожидаемое число лет, прожитых между возрастами x и x + 1 дожившими до возраста х лицами из исходной группы, содержавшей lo новорожденных. Мы имеем
(5.11)
где интеграл в правой части равен числу лет, прожитых теми, кто умер в возрастном интервале между х и х+1, a lx+1 равно числу лет, прожитых в возрастном интервале между х и х + 1 теми, кто дожил до возраста х + 1.
Интегрирование по частям дает
(5.12)
Функция Lx также используется в определении повозрастного коэффициента смертности в интервале между х и х + 1, который обозначается через mx , где
(5.13)
Приведенные выше определения для mx и Lx можно распространить на воз растные интервалы длины, отличной от единицы:
(5.14)
(5.15)
Для совокупности случайного дожития nLx является общим ожидаемым числом лет, которые прожиты в возрастном интервале между х и х + n дожившими до возраста ж лицами из исходной группы, содержавшей l о новорожденных, а nmx является повозрастным коэффициентом смертности, наблюдавшимся в этой группе на интервале (х, х + n).
Символ Tx обозначает общее число лет, прожитых после достижения возраста х лицами, дожившими до этого возраста, из исходной группы, содержавшей l0 новорожденных. Мы имеем
(5.16)
Последнее выражение можно интерпретировать как интеграл от общего времени, прожитого между возрастами x + t и x + t + dt группой из lx+t лиц, которые дожили до этого возрастного интервала. Обратим также внимание, что Tx является пределом величины nLx , когда n стремится к бесконечности.
Среднее число лет предстоящей жизни для lx лиц из группы, доживших до возраста x, определяется выражением
в соответствии с формулами (5.1) и (5.2).
Мы можем найти выражение для среднего числа лет, прожитых между возрастами х и х + n группой из lx лиц, доживших до возраста х:
(5.17)
Эта функция является усеченной (на n-летнем интервале) полной ожидаемой продолжительностью жизни для лиц (х) и обозначается через .
Последней функцией, связанной с описанной в этом разделе интерпретацией таблицы смертности, является среднее число лет, прожитых между возрастами х и х + 1 теми лицами в группе доживших до возраста х, которые умирают в некоторый момент между этими возрастами. Эта функция обозначается через α(х) и определяется соотношением
(5.18)
При вероятностном взгляде на таблицы смертности мы получили бы
Если мы предполагаем, что
т. е. если моменты смерти равномерно распределены внутри годичного возрастного интервала, то мы получим
Это обычное приближение функции α(х), пригодное для лиц всех возрастов, кроме совсем юных и очень старых, где, как показывает рис. 3.2, это предположение может не соответствовать действительности.
Пример 5.1. Покажем, что
Решение. Из (5.11), (5.12) и (5.18) мы получаем
или
Формулу можно обосновать, приближая интеграл в (5.12) с помощью формулы трапеций
5.2. Рекуррентные формулы
Пример 5.1 иллюстрирует применение численного анализа для нахождения характеристик таблиц смертности. Для приближенного интегрирования используется формула трапеций.
Для иллюстрации другого вычислительного метода, который использует рекуррентные формулы, рассмотрим вычисление полных и пошаговых ожидаемых продолжительностей жизни. При применении рекуррентных формул будем использовать одну из двух следующих форм:
обратная рекуррентная формула
(5.19)
или
прямая рекуррентная формула
(5.20)
Переменная х обычно принимает целые неотрицательные значения.
Таблица 5.1. Обратные рекуррентные формулы для ex и
Для вычисления функции u(х) при целых неотрицательных значениях х нам нужно знать соответствующие значения функций с(х) и d(x) и начальное значение функции и(х) . Эта процедура используется в последующих главах и иллюстрируется в табл. 3.5.1, где для вычисления ex и применяются обратные рекуррентные формулы.
6. Предположения для дробных возрастов
Ранее мы обсуждали непрерывную случайную величину Т, продолжительность предстоящей жизни, и дискретную случайную величину К, пошаговую продолжительность предстоящей жизни.
Таблица смертности, представленная в разделе 3, полностью определяет распределение вероятностей с.в. К. Для определения распределения с.в. Т мы должны постулировать некоторую аналитическую форму или основываться на таблице смертности, приняв некоторое предположение о структуре распределения между целыми точками.
Рассмотрим три широко используемых в актуарной науке предположения. Они будут сформулированы в терминах функции дожития и в такой форме, которая позволяет показать природу интерполяции на интервале (х,х + 1), вытекающую из каждого из этих предположений. В каждом утверждении х является целым и 0<=t<=1. Сформулируем предположения:
• Линейная интерполяция: s(x + t) = (1 — t) s (x) + t s(x + 1). Это приводит к равномерному распределению или, точнее, к равномерному распределению моментов смерти внутри каждого годичного возрастного интервала. При этом предположении tPxявляется линейной функцией.
• Показательная интерполяция, или линейная интерполяция для ln(s(x + t) : ln(s(x — 1)) = (1 — t)ln(s ( x ) + t ln(s ( x + 1)). Это согласуется с предположением о постоянной интенсивности смертности внутри каждого годичного возрастного интервала. При этом предположении tPxявляется показательной функцией.
• Гармоническая интерполяция: ln(x + t) = (l — t)ln(s(x))+ t ln(s( x+ l)). Это то, что называется предположением о гиперболичности (исторически, предположением Балъдуччи, поскольку в этом случае tPxявляется гиперболической кривой.
Опираясь на эти основные определения, для остальных стандартных вероятностных функций можно вывести формулы в терминах вероятностей, указанных в таблице смертности.
Такие результаты представлены в табл. 6.1. Заметим, что мы с тем же успехом могли бы сформулировать эквивалентные определения в терминах функции плотности, функции распределения или интенсивности смертности.
Вывод выражений, входящих в табл. 6.1, является просто упражнением, заключающимся в подстановке сформулированных выше предположений о s(x + t) в соответствующие формулы разделах 2 и 3. Мы продемонстрируем этот процесс для равномерного распределения смертей. Для определения первого выражения в столбце, относящемся к равномерному распределению, начнем с соотношения
а затем подставим соответствующее выражение для s( x + t ) и получим
Для второго выражения воспользуемся формулой (2.13) и
далее, подставляя соответствующее выражение для s( x + t), получаем
Деление числителя и знаменателя в правой части на s( x ) приводит к формуле
Третье выражение является частным случаем четвертого при у = 1 — t . Рассматривая четвертое выражение, начнем с равенства
затем, подставив соответствующее выражение для s( x + t) и s(x + t + у) , получим
Пятое выражение является дополнением первого, и последнее выражение в столбце, относящемся к равномерному распределению, является произведением второго и пятого выражений.
Таблица 6.1. Вероятностные функции для дробных возрастов
Если, как и ранее, х является целым числом, то анализ можно провести, введя случайную величину S = S( x ), такую, что
T=K+S (6.1)
Где Т является продолжительностью предстоящей жизни, К — пошаговой продолжительностью предстоящей жизни, a S — случайной величиной, представляющей прожитую дробную часть года, в котором наступила смерть.k + s) = kPx sPx+k .
Теперь, воспользовавшись выражением для s q x +k в предположении равномерности распределения, как показано в табл. 6.1, получим
P[(K = k)∧(S<=s)] = kPx sPx+k = k|qxs = P(K = k)P(S<=s)… (6.2)
Таким образом, совместное распределение св. К и S может быть разложено на произведение маргинальных распределений с.в. К и S. Поэтому в предположении равномерности распределения моментов смерти с.в. К и S оказываются независимыми. Поскольку распределение P(S<=s) = s является равномерным на (0,1), св. S имеет именно такое равномерное распределение.
Пример 6.1. Будут ли св. К и S независимыми в предположении постоянной интенсивности смертности?
Решение. Воспользовавшись информацией из табл. 6.1, относящейся к пред- пол ожению о постоянной интенсивности смертности, мы получаем
P[(K = k)∧(S<=s)] = kPx sPx+k = kPx [1 — (рx+k)s ]
Для обсуждения этого результата будем различать два случая:
• если в выражение для рx+kвходит к , то мы не можем представить совместное распределение св. К и S в виде произведения маргинальных распределений. Отсюда мы делаем вывод, что с.в. К и S не являются независимыми.
• в частном случае, когда рx+k = рx— константа,
Для этого частного случая мы получаем, что с.в. К и S оказываются независимыми в предположении постоянной интенсивности смертности. Ў
Пример 6.2. Покажем, что в предположении равномерности распределения смертей
Решение. (a)
(b) D[T] = D[K+S]. Из независимости св. К и 5 в предположении равномерности распределения смертей получаем D[T] = D[K] + D[S]. Далее, поскольку с.в. S равномерно распределена на (0,1), D[T] = D[K] + 1/2. Ў
7. Некоторые аналитические законы смертности
Имеется три основных аргумента в пользу принятия аналитического выражения для функции смертности или для функции дожития.
Первый — философский. Многие явления, изучавшиеся в физике, можно эффективно объяснить с помощью простых формул. Поэтому, основываясь на биологических соображениях, некоторые авторы предположили, что дожитие в человеческом сообществе управляется такими же простыми законами.
Второй аргумент — практический. Функция с несколькими параметрами легче воспринимается, чем таблица смертности с, возможно, 100 параметрами или вероятностями смерти.
Кроме того, некоторые из аналитических выражений обладают простыми свойствами, которые удобны при выводе вероятностных утверждений, касающихся более чем одного лица.
Третий аргумент для простых аналитических функций дожития — легкость оценивания параметров этой функции на основе данных о смертности.
В последние годы энтузиазм в отношении простых аналитических функций дожития существенно уменьшился. Многие полагают, что вера в универсальные законы смертности наивна. При все увеличивающемся быстродействии и объеме памяти компьютеров преимущества некоторых аналитических выражений при проведении вычислений, касающихся более чем одного лица, уже не играют значительной роли.
Однако в результате некоторых недавних исследований оживились биологические аргументы в поддержку аналитических законов смертности.
В табл. 7.1 приводятся несколько семейств простых аналитических функций смертности и дожития, соответствующих различным известным законам. Для удобства ссылок указаны названия законов, лежащих в их основе, и даты публикации.
Таблица 7.1. Функции смертности и дожития для различных распределений
|
Исходное распределение
|
μ(x)
|
s(x)
|
Ограничения
|
|---|---|---|---|
|
Де Муавр (1729)
|
(ω-x)-1
|
1-x/ω
|
0 <= x<ω
|
|
Гомперц (1825)
|
Всx
|
ехр[-m(сx-1)]
|
В > 0, с > 1, х>О
|
|
Мейкем (1860)
|
А+Всx
|
ехр[-Аx-m(сx-1)]
|
В > 0, А >= -В, с > 1, x>0
|
|
Вейбулл (1939)
|
kxn
|
exp(-uxn+1 )
|
k>0, n>0, x>=0
|
Отметим следующие факты:
• специальные символы определяются формулами m =B/ln(c), u=k/(n+1).
• закон Гомперца является частным случаем закона Мейкема при А = 0.
• если с = 1 в законах Гомперца и Мейкема, то мы приходим к показательному (постоянная интенсивность смертности) распределению.
• при рассмотрении закона Мейкема считалось, что константа А отвечает несчастному случаю, а выражение Всx— старению.
Выражения в столбце s(x) табл. 7.1 были получены подстановкой в (2.16). Например, для закона Мейкема
где m = В/ In с.
Селекционные и заключительные таблицы
В разд. 2 рассматривалось, как можно двумя способами интерпретировать величину tPx, вероятность того, что лицо (х) доживет до возраста х + t.
Первая интерпретация состояла в том, что эту вероятность можно вычислить на основе функции дожития для новорожденных при единственном предположении, что новорожденный доживет до возраста х. Эта интерпретация стала основой для обозначений и для выведения формул.
Вторая интерпретация состояла в том, что дополнительная информация о лице возраста х может сделать исходную функцию дожития непригодной для вычисления вероятностных утверждений о продолжительности предстоящей жизни лица (х) .
Например, некоторое лицо может пройти обследование и быть принятым на страхование в возрасте х. Наличие этой информации позволило бы считать, что распределение продолжительности предстоящей жизни лица (x) отличается от того, которое мы считали бы подходящим для лица возраста х, если бы не располагали этой информацией.
Второй пример: некоторое лицо может стать инвалидом в возрасте х. Эта информация позволяет нам предполагать, что распределение продолжительности предстоящей жизни лица (х) отлично от соответствующего распределения для лица, не ставшего инвалидом в возрасте х.
В этих двух примерах следует отдать предпочтение специальной интенсивности смертности, учитывающей конкретную информацию, которая становится известной в возрасте х. Без этой конкретной информации об (х) интенсивность смертности по прошествии времени t будет функцией только достигнутого возраста х + t, что в предыдущем разделе обозначалось через μ(х + t ).
Если известна дополнительная информация в момент х , то интенсивность смертности в момент х + tявляется функцией этой информации в момент х и величины t . Мы будем обозначать ее через μx(t), где отдельно указывается возраст х, в котором была доступна дополнительная информация, и величина t . Сама дополнительная информация в явной форме в это обозначение не входит, но ясна из контекста.
Другими словами, полная модель для таких лиц является набором функций дожития, по одной для каждого возраста, в котором имеется информация о принятии на страхование, об инвалидности и т. п. Это множество функций дожития можно воспринимать как функцию двух переменных.
Одна переменная — возраст в момент селекции (например, в момент выдачи страхового договора или наступления инвалидности) [х] и вторая переменная — время, прошедшее с момента выдачи договора или с момента селекции t . Тогда каждая из обычных функций таблицы смертности, отвечающая такой функции от двух пере менных, является двумерным массивом по [х] и t .
Мы используем здесь квадратные скобки, чтобы отметить переменную, относящуюся к возрасту, в котором проводилась селекция. Когда наличие селекции явствует из интенсивности смертности, мы будем опускать квадратные скобки, чтобы не усложнять обозначения.
Схематическая диаграмма на рис. 8.1 иллюстрирует эти соображения. Например, предположим, что имеется некоторая специальная информация о группе лиц возозраста 30 лет. Может быть, они были приняты на страхование, а может быть, стали инвалидами.
Для этих лиц можно построить специальную таблицу смертности.
Условная вероятность смерти в каждый год с момента селекции будет обозначаться q[30]+i i = 0,1,2,…, и будет входить в первую строку на рис. 8.1. Индекс сражает двумерную природу этой функции, где в квадратные скобки заключен возраст тридцать лет, [30], т. е. функция дожития в первой строке опирается на специфическую информацию, имеющуюся в возрасте 30 лет.
Вторая строка на рис. 8.1 будет содержать вероятности смерти для лиц, относительно которых специфическая информация стала известной к возрасту 31. В актуарной науке такая двумерная таблица смертности называется селекционной таблицей смертности
путь для совокупности дожития, прошедшей сеекцию в возрасте [х]
линия, связывающая ячейки для лиц, достигших одинакового возраста, по прошествии 15 лет с момента селекции
другой путь для совокупности дожития по прошествии 15 лет с момента селекции; эти вероятности составляют заключительную таблицу смертности
Рис. 8.1. Селекционная, заключительная и агрегативная смертность, 15-летний период селекции
Замечания
• в биостатистике индекс [х] селекционной таблицы не обязан быть возрастом. Например, в исследованиях онкологических заболеваний [х] может быть классификационным индексом, который зависит от размера и местоположения опухоли, и время после селекции будет отсчитываться от момента постановки диагноза.
• заключительную смертность, после 15-летнего периода селекции, для возраста [x] + 15 следует оценивать, используя наблюдения из всех ячеек, вида [х — j]+ 15 + j , j = 0,1,2,…. Поэтому q[x]+15 = qx+15оценивается взвешенным средним оценок смертности по различным группам селекции. Если эффект селекции достаточно ве
лик, то на получаемую оценку будут влиять данные из различных ячеек.
Влияние селекции на распределение продолжительности предстоящей жизни Т может уменьшаться по мере удаления от момента селекции. Вне некоторого времен ного интервала величины q для лиц одинакового возраста будут по существу равны вне зависимости от возраста в момент селекции.
Точнее, если имеется наименьшее целое число r, такое, что |q[x]+r-q[x-j]+r+j| меньше, чем некоторая маленькая положительная постоянная, для всех возрастов селекции [х] и для всех j > 0, то было бы экономично построить множество селекционных и заключительных таблиц, срезая двумерный массив после колонки r + 1.
Для временных интервалов, превосходящих г, мы можем использовать соотношение
Первые r лет после момента селекции составляют период селекции.
Получающийся массив содержит некоторое множество таблиц смертности, по одной на каждый возраст селекции, причем для одного возраста селекции элементы таблицы смертности расположены по горизонтали в течение периода селекции, а затем по вертикали в заключительный период. Это показано на рис. 8.1 стрелками.
В исследованиях смертности, проводившихся Обществом актуариев для лиц, которые были застрахованы по стандартному договору индивидуального страхования жизни, использовался 15-летний период селекции (см. рис. 8.1), т. е. считается, что
За пределами периода селекции вероятности смерти снабжаются одним индексом, достигнутым возрастом, т.е. вместо q[x-j]+r+jпишется qx+r — Например, при r = 15 и вместо q[30]+15 и вместо q[25]+20 пишется q45.
Таблица смертности, в которой функции даются только для достигнутых возрастов, называется агрегативной таблицей. Такой, например, является табл. 3.1. Последний столбец в селекционной и заключительной таблице является специальной агрегативной таблицей, которая обычно называется заключительной таблицей, что отражает использование селекции.
Таблица 8.1 содержит вероятности смерти и соответствующие значения функций l[x]+ k из издания «Permanent Assurances , Females , 1979-82, Tables», опубликованного Институтом и факультетом актуариев Великобритании.
Ее называют таблицей AF 80. У этой таблицы двухлетний период селекции, и ее проще использовать для иллюстраций, чем таблицы с 15-летним периодом, такие, как «Основные таблицы», опубликованные Обществом актуариев США.
Таблица 8.1. Выдержка из селекционной и заключительной таблицы AF 80
|
|
(1)
|
(2)
|
(3)
|
(4)
|
(5)
|
(6)
|
(7)
|
|---|---|---|---|---|---|---|---|
|
[x]
|
1000q[x]
|
1000q[x]+1
|
1000qx+2
|
lx
|
lx+1
|
lx+2
|
x+2
|
|
30
|
0,222
|
0,330
|
0,422
|
9906,7380
|
9904,5387
|
9901,2702
|
32
|
|
31
|
0,234
|
0,352
|
0,459
|
9902,8941
|
9900,5769
|
9897,0919
|
33
|
|
32
|
0,250
|
0,377
|
0,500
|
9898,7547
|
9896,2800
|
9892,5491
|
34
|
|
33
|
0,269
|
0,407
|
0,545
|
9894,2903
|
9891,6287
|
9887,6028
|
35
|
|
34
|
0,291
|
0,441
|
0,596
|
9889,4519
|
9886,5741
|
9882,2141
|
36
|
В табл. 8.1 мы имеем три вероятности смертности для возраста 32, а именно
q[32] = 0,000250 < q[31]+1 = 0,000352 < q32= 0,000422.
Упорядочение этих вероятностей понятно, поскольку смертность для лиц, только что принятых на страхование на случай смерти, должна быть ниже. Можно считать, что столбец (3) предоставляет информацию о заключительных вероятностях смертности.
Если заданы одногодичные коэффициенты смертности в селекционной и заключительной таблице, то построение соответствующей селекционной и заключительной таблицы смертности (функций дожития) начинается с заключительной части.
Далее могут использоваться такие формулы, как (4.1), которые дадут множество величин lx+r=l[x]+r, r является длиной периода селекции. Мы завершим рассмотрение селекционных частей, воспользовавшись соотношениями
двигаясь от r — 1 к 0.
Пример 8.1. Воспользовавшись табл. 8.1, вычислим:
Решение.Формулы, полученные ранее, можно приспособить к селекционным и заключительным таблицам, получив
В начало
Содержание портала
Трапеция | Блог по математике ∞
Трапеция — это плоская форма с четырьмя прямыми сторонами. Две стороны параллельны друг другу и противоположны друг другу. Трапеция не обязательно должна быть маленькой, так как длина сторон и углы могут сильно различаться. В то время как некоторые люди думают, что трапеция — это термин, зарезервированный исключительно для учебников по математике, реальные примеры трапециевидных форм можно найти в сумках, опорах мостовых ферм, банках для попкорна и некоторых музыкальных инструментах, таких как гитарные цимбалы..
Студенты иногда путаются, когда дело доходит до определения площади трапеции, просто потому, что они не знают, как правильно обозначить форму, чтобы они могли вставить правильные числа в формулу. Эти ключевые факты помогут определить правильные числа для использования в формуле для определения площади трапеции:
Две стороны, идущие параллельно друг другу, называются основаниями.
Две другие стороны называются ножками.
Расстояние между двумя базами называется высотой или высотой.
При нахождении площади трапеции необходимо следовать простой формуле. Если вы укажете правильные числа в формуле и не сделаете простых ошибок при сложении, делении и умножении, вы легко сможете прийти к окончательному ответу. Формула выглядит следующим образом:
Площадь = a + b x h
2
Верхняя базовая линия обозначается как «а».
Нижняя базовая линия обозначается буквой «b».
Высота обозначается как «h.”
Пример. Предположим, у нашей трапеции есть основания длиной 6 метров и 8 метров и высотой 4 метра, поэтому наша формула будет выглядеть так.
6 м + 8 м x 4 м
2
Шаг 1: Сначала необходимо сложить две базы. Итак, мы говорим 5м + 8м = 14м.
Шаг 2: Разделите число, полученное при сложении оснований, на 2. Итак, вы скажете 14, разделенное на 2, что равно 7.
Шаг 3: возьмите 7 и умножьте на «h», что равно 4.
Ответ: Ответ на эту проблему — 28 м2
При поиске площади трапеции важно не перепутать числа и поставить их на их законное место в формуле, чтобы можно было найти нужную область. Если вы перепутаете одно число, вы получите совершенно неправильный ответ, даже если вы знаете правильную формулу.
Трапеции обычно встречаются в дизайне мебели, такой как столы, и в других объектах, таких как знаки. Есть много причин, по которым человеку может потребоваться найти область объекта, например, планирование строительного проекта, покраска и изготовление покрытия для стола.
Интересный факт:
Часто возникает путаница, когда дело доходит до значения трапеции и того, что этот термин означает в США и Великобритании. В США этот термин означает четырехугольник с одной парой параллельных сторон, в то время как в Великобритании трапеция не имеет параллельных сторон.
Что такое трапеция? [Определение, факты и пример]
Что такое трапеция?
Трапеция, также известная как трапеция, представляет собой плоскую замкнутую форму, имеющую 4 прямые стороны с одной парой параллельных сторон.
Параллельные стороны трапеции называются основаниями, а непараллельные стороны — ножками. У трапеции тоже могут быть параллельные ножки. Параллельные стороны могут быть горизонтальными, вертикальными или наклонными.
Расстояние по перпендикуляру между параллельными сторонами называется высотой.
Примеры :
Без примеров :
Типы трапеций
Трапеция бывает трех типов, а именно
1. Правая трапеция : Имеет пару прямых углов.
2. Равнобедренная трапеция : Имеет равные длины непараллельных сторон. На изображении стороны AD и BC равны.
3. Чешуйчатая трапеция : у нее нет равных углов и равных сторон.
Свойства трапеции
Трапеция называется параллелограммом, если обе пары ее противоположных сторон параллельны.
Трапеция — это квадрат, если обе пары его противоположных сторон параллельны; все его стороны равной длины и расположены под прямым углом друг к другу.
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу.
Примеры из реальной жизни
Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов.
Интересные факты
|
примеров трапеций в реальной жизни
Трапеции | математика ∞ блог. Во-вторых, кого вы подозреваете в том, что он трапеция в реальной жизни? | Справка. Таблица Ежедневно добавляются тысячи новых качественных картинок.
Это примеры того, как формы встречаются в окружающей среде. Числовая интеграция — правило трапеции Maplesoft, подразделение Waterloo Maple Inc., 2007. Есть несколько реальных примеров трапеции, которые можно встретить каждый день.
Coo Coo Clock. каков реальный пример трапеции? Трапециевидную форму можно увидеть в конструкции моста с фермой, такой как этот. Поскольку трапеция не может быть трехмерной, многие реальные примеры трапеций имеют такую форму лишь частично. На баскетбольных площадках видны трапециевидные знаки. Отсюда следует, что ∫ ≈ (-) ⋅ + (). 4 ответа. 0 0 0. Решенный пример на трапеции Вопрос: Трапециевидная клумба имеет параллельные стороны длиной 12 м и 6 м. Найдите площадь клумбы, если ее высота 8 м.Варианты: A. Решенный пример на трапеции. Вопрос: Трапециевидная клумба имеет параллельные стороны длиной 12 м и 6 м. Найдите площадь клумбы, если ее высота 8 м. Выбор: A. Какие примеры трапеций из реальной жизни? Например, поверхность стола может иметь форму трапеции, а его ножки и опоры — нет.
Трапеция — это четырехугольник с одной парой параллельных сторон. 76 м 2 B. Источник (и): реальная трапеция: https://tr.im/LWYzS. Реальные примеры трапеций включают некоторые столешницы, опоры для мостов, боковины сумок и архитектурные элементы.Коробка попкорна. Некоторые из многих примеров трапеции — это лицевая сторона коробки для попкорна, сумочки и мостов. Нет, трапеция — это четырехугольник, у которого ровно ОДНА пара параллельных сторон. К ним относятся 21 цветное и черно-белое изображение. Фонарь. Этот сайт может вам помочь.
Тоблерон, кусок торта или пирога … Трапеция — многоугольник? Кошелек. 1 десятилетие назад. Крылья этого самолета — трапециевидные. Что представляет собой пример четырехугольника в реальной жизни (помимо воздушного змея. Правило трапеции работает, аппроксимируя область под графиком функции как трапецию и вычисляя ее площадь.Определение словаря трапеции | трапеция определена.
Поскольку трапеция не может быть трехмерной, многие реальные примеры трапеций имеют такую форму лишь частично.
В реальном мире существует так много различных типов квадратов. Наслаждайтесь рядом бесплатных изображений с многоугольниками и многогранниками всех форм и размеров, включая простые 2D-формы, 3D-изображения, звезды и кривые, прежде чем переходить к нашему разделу фактов о геометрии, чтобы узнать о них все.Любимый ответ. Примеры из реальной жизни. Эдгар Гринберг. 1. Ответьте «Сохранить». каков реальный пример трапеции?
Реальные примеры трапеций включают некоторые столешницы, опоры для мостов, боковины сумок и архитектурные элементы. Прямоугольный треугольник 10. Это известное произведение искусства состоит из множества различных прямоугольных треугольников. 1. Это реальный пример прямоугольного треугольника, потому что стена и земля являются опорами, а лестница — гипотенузой. Кашпо для цветов. Правильная форма трапеции.Это приложение — один из коллекции примеров обучения исчислению с Maple. 5 лет назад. Актуальность. В этот набор входят изображения: трапеции красного, зеленого, синего и желтого цветов. Другими словами … Какие примеры иронии из реальной жизни? Решение: Шаг 1: Клумба в форме трапеции 1 десятилетие назад. Изображение трапеции. 72 м 2 C. 68 м 2 D. 74 м 2 Правильный ответ: B. Примеры видео: Геометрия — Трапеции. Найдите стоковые изображения трапеции в формате HD и миллионы других стоковых фотографий, иллюстраций и векторных изображений без лицензионных отчислений в коллекции Shutterstock.Авторизуйтесь, чтобы ответить на ответы Пост; Анонимный. Com. Powered by Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. RE: каков реальный пример трапеции? Трапеции в реальном мире!
Трапеция может быть прямоугольником, если обе пары ее противоположных сторон параллельны; его противоположные стороны равны по длине и расположены под прямым углом друг к другу. 9.Эта настоящая живая картинка показывает, как гора
Наружный свет. Трапеция. 0 0 0. ∫ (). 72 м 2 В. 68 м 2 Г. 74 м 2 Правильный ответ: Б.
Где в мире трапеция трапеция?
Как учитель, я помню, как бесконечно говорил о квадратах на одном дыхании, как о том, что «квадраты — это особый тип прямоугольников». Я часто разрабатывал задания, в результате которых ученики создавали древовидные диаграммы или диаграммы Венна, чтобы показать семейную классификацию четырехугольников. Будь то углы, размеры, меры, конструкции или представление неизвестных величин, формы можно было регулярно видеть на уроках.
При проектировании путевых точек геометрии в Кембриджской математической системе я обнаружил большое количество исследований, касающихся классификации четырехугольников.Большая часть этого исследования выявляет проблемы, с которыми мы слишком хорошо знакомы: ученики не осознают, что квадрат — это тип прямоугольника, а прямоугольник — это тип параллелограмма; необходимые и достаточные свойства четырехугольника и характеристики форм перечислить несколько. Ученики редко полностью понимают или знают истинное математическое определение каждого четырехугольника, и вместо этого склонны перечислять их характеристики, четыре стороны и все остальное.
Следует отметить несколько особенностей. Некоторые мутят воду, а другие помогают нам решить проблемы.Имея это в виду, вот небольшой набор важных вопросов, о которых следует подумать, когда вы работаете в этой области.
Какое определение для трапеции? У фигуры ровно одна пара параллельных сторон или хотя бы одна пара параллельных сторон? А может, вообще ничего! В разных культурах трапеции определяются по-разному, и во многих тоже есть термин трапеция. В США (для некоторых) трапеция — это четырехсторонний многоугольник без параллельных сторон; в Великобритании трапеция — это четырехсторонний многоугольник с ровно одной парой параллельных сторон; в то время как в Канаде трапеция имеет инклюзивное определение, так как это четырехсторонний многоугольник, по крайней мере, с одной парой параллельных сторон — следовательно, параллелограммы — это особые трапеции.
Сейчас я не в состоянии принять окончательное решение по этому поводу, но указать, что эти проблемы существуют (особенно в мультикультурных классах, в которых мы преподаем), важно, как и указывает тем, кто ищет в Интернете, когда урок Планируя, что часто требуется некоторая осторожность, внимание и скептицизм!
Евклид, прародитель большей части нашей школьной программы по геометрии, определил (Книга 1, определение 2) квадрат, имеющий равные стороны и прямые углы, продолговатый, чтобы иметь четыре прямых угла, но не четыре равных стороны, ромб, чтобы иметь четыре равных угла. стороны, но без прямых углов, ромб имеет равные противоположные стороны и равные противоположные углы, но без прямых углов и без четырех равных сторон.Все остальные четырехугольники имели форму трапеции.
Даже простое осмысление этого — прекрасная возможность по-настоящему подумать о том, как выглядят эти формы и их знакомые отношения, поскольку Евклид подразумевает, что на самом деле нет никаких пересечений между формами. Каждый из них представляет собой квадрат, продолговатую форму, ромб, ромб или трапецию. Разве это не упростило бы жизнь?
Ну да и нет. Возникает вопрос, почему у нас есть те всеобъемлющие определения, которые у нас есть? Какой в этом смысл — неужто они просто ошеломляют и сбивают с толку?
Все сводится к тому, что мы можем вывести и заключить от одной формы к другой.Квадрат — это особый тип прямоугольника и ромба и, следовательно, особый параллелограмм. Эти иерархические определения приводят к более экономичным определениям понятий и формулировкам теорем, упрощают дедуктивную систематизацию и вывод свойств более специальных понятий, обеспечивают полезную концептуальную схему при решении проблем, могут предлагать альтернативные определения и новые предложения и обеспечивать полезные глобальные перспективы ( Де Вильерс, 1994).
Другими словами: теорема, которую вы доказываете для параллелограмма, верна для квадратов, прямоугольников и ромбов, поскольку все они являются типами параллелограмма.Однако теорема, которая верна для квадрата, может не выполняться для всех параллелограммов, поскольку не все параллелограммы являются квадратами.
Здесь действительно интересно взглянуть на ограничения, необходимые при передаче семейства параллелограммов; рассмотреть, что остается инвариантным и как это взаимодействует с рассматриваемой теоремой. Возможно, ваше доказательство, основанное на квадрате, не основывается на этих жестких ограничениях, которые делают квадрат не просто параллелограммом, поэтому на самом деле ваше доказательство будет работать для всех параллелограммов.
При поиске чудес Интернета Википедия предлагает эту замечательную диаграмму:
https://upload.wikimedia.org/wikipedia/commons/9/9a/Euler_diagram_of_quadrateral_types.svg
Возможно, вы не полностью согласны с используемыми названиями, но замечательно то, как вы можете определить ужесточение или ослабление ограничения во время прогулки. Оставьте область, и вы расслабитесь, войдите в другой слой и затяните. Это также подчеркивает, что на самом деле, вы знаете, может быть, продолговатый — не такое уж неприятное слово — продолговатые и квадраты составляют семейство прямоугольников, а «продолговатый» может помочь с целыми квадратами — это путаница с прямоугольниками.В качестве альтернативы Клементс и Сарама (2009) предлагают использовать двойное имя квадрат-прямоугольник. Означает ли это, что у нас также будут ромб-параллелограммы? Было бы неплохо подумать, действительно ли некоторые регионы пусты, и у нас, как у команды, есть вопрос, следует ли включать «дартс» здесь и в кайт-регион?
Весь разговор просто подчеркивает, насколько запутанным может быть определение четырехугольника. Крайне важно решить, что мы считаем необходимыми и достаточными условиями, и, следовательно, знакомыми отношениями, и в то же время быть готовыми изложить их явно.Может быть, как только мы это сделаем, мы сможем нарисовать нашу собственную диаграмму Википедии для наших определений. Я оставлю это вам один раз, но мне было бы интересно, что вы создаете! Могу я найти ваши определения из вашей диаграммы?
Артикул:
Клементс, Д.Х., Сарама, Дж., 2000. Идеи маленьких детей о геометрических формах. Обучение детей математике 6, 482–488.
Де Вильерс, М., 1994. Роль и функция иерархической классификации четырехугольников. Для изучения математики 14, 11–18.
Сарама, Дж., Клементс, Д.Х., 2009. Форма, в: Математическое образование и исследования для детей младшего возраста, Траектории обучения для детей младшего возраста. Рутледж, Нью-Йорк, стр. 199–246.
ЧТО-ТО ПОПРОБОВАТЬ: KS1: Что общего у каждого набора фигур? Что отличает каждый от другого? KS2: Прямоугольник — это особый тип параллелограмма. Почему? KS3: Нарисуйте древовидную диаграмму, чтобы связать семейство четырехугольников.Объясните ссылки, которые вы сделали. KS4: построить циклический параллелограмм. KS5: Теорема Ван Обеля утверждает, что: Если квадраты построены на сторонах любого четырехугольника, то отрезки прямых, соединяющие центры противоположных квадратов, равны и перпендикулярны. Какую форму образовали бы эти центры, если бы исходный четырехугольник был параллелограммом? Использование иерархических классификаций покажет, почему. Рассмотрим здесь доказательства исходной теоремы. |
Трапеции: определение и свойства — стенограмма видео и урока
Свойство
Трапеции имеют одно свойство, которое необходимо соблюдать.Свойство в том, что у него должна быть одна пара параллельных сторон. Если вы посмотрите на трапецию, вы увидите, что у нее две плоские стороны. Эти плоские стороны параллельны друг другу. Если вы продлите эти линии, они никогда не встретятся. Попытайся.
Словарь
При работе с трапециями есть несколько слов, которые мы должны добавить в наш словарь.
Первое слово — это оснований , которые являются сторонами, параллельными друг другу. Нарисуйте треугольник, нижняя сторона которого будет одной из ваших основ.Сторона, полученная путем срезания вершины треугольника, является другой основой.
Второе слово, которое следует учитывать, — это ножек . Это наклонные стороны, которые образуют левый и правый край трапеции, которая находится самой длинной стороной вниз. Возвращаясь к разрезанному треугольнику, ноги — это стороны, которые поднимаются и встречаются на вершине треугольника. Но, поскольку вершина треугольника срезана, ноги заканчиваются там, где произошел срез.
Третье слово — высота , что просто высота трапеции.Это то, насколько высока трапеция, когда вы сидите на плоской поверхности. Вы можете определить высоту, измерив расстояние от одной базы до другой.
Специальные трапеции
Когда ноги вашей трапеции имеют одинаковую длину и когда углы, которые каждая сторона образует с основанием, равны, тогда у вас есть так называемая равнобедренная трапеция . Это означает, что, если трапеция расположена ровно с самым длинным основанием вниз, два нижних угла будут равны, а два верхних угла также будут равны.Представьте себе эту трапецию как равнобедренный треугольник (треугольник с двумя равными сторонами и двумя равными углами) с отрезанной вершиной.
Теперь представьте себе разносторонний треугольник (треугольник, все стороны которого имеют разную длину) и отрежьте его вершину. Когда вы это сделаете, вы получите разностороннюю трапецию , трапецию, ноги которой имеют разную длину.
Третий вид специальной трапеции — это правая трапеция , трапеция, у которой одна ножка перпендикулярна основанию.Он будет выглядеть как прямоугольный треугольник (треугольник с одним прямым углом) с обрезанной вершиной.
Краткое содержание урока
Вау! Посмотрите, что мы узнали всего за несколько минут! Мы узнали, что трапеция представляет собой четырехстороннюю плоскую форму с одной парой параллельных сторон. Трапеции выглядят как треугольники со срезанной вершиной. Единственное свойство, которому должны соответствовать все трапеции, — это то, что у них должны быть две стороны, параллельные друг другу.
Специальные слова, которые мы используем с трапециями, — это основания, ноги и высота. Основания относятся к двум сторонам, параллельным друг другу. Ножки относятся к двум наклонным сторонам, а высота — это просто высота трапеции, когда она расположена ровно с опущенным самым длинным основанием.
Особый случай равнобедренной трапеции возникает, когда у вас есть ноги, равные по длине друг другу, и углы, образованные ногами и основаниями, также равны друг другу. Итак, у равнобедренной трапеции два нижних и два верхних угла равны друг другу.Особый случай разносторонней трапеции возникает, когда обе ножки имеют разную длину, а правая трапеция возникает, когда одна ножка перпендикулярна основанию.
Результаты обучения
Усвоение информации из этого урока может привести к вашей способности:
- Распознавать свойство, связанное с трапециями
- Определите основания, опоры и высоту, как они соотносятся с трапециями
- Характеризуйте особые трапеции: равнобедренную, разностороннюю и правую
Определение, типы, свойства, площадь и периметр, решенные примеры, практические вопросы, часто задаваемые вопросы
Трапеция завораживает, потому что определяется в зависимости от того, к какому географическому положению вы принадлежите.Если вы приехали в Соединенное Королевство в рамках поездки по обмену и попросите одного из учащихся нарисовать вам трапецию, они нарисуют ее как трапецию. Трапецию также называют трапецией в некоторых частях мира, и это тип четырехугольника с одной парой противоположных сторон, параллельных друг другу.
Определение трапеции
Трапеция — это четырехсторонняя замкнутая двухмерная фигура, имеющая площадь и периметр. Две стороны трапеции параллельны друг другу, и они называются основаниями трапеции.Непараллельные стороны известны как ноги или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой. Поскольку противоположные стороны параллельны друг другу, вычислить площадь трапеции несложно.
Свойства трапеции
Это свойства трапеции, которые выделяют ее среди других четырехугольников:
- Основания (верх и низ) параллельны друг другу
- Противоположные стороны трапеции (равнобедренные) одинаковой длины
- Сумма углов рядом друг с другом составляет 180 °
- Медиана параллельна обоим основаниям
- Длина медианы — это среднее значение обоих оснований i.е. (а + б) / 2
- Если обе пары противоположных сторон параллельны трапеции, она считается параллелограммом
- Если обе пары противоположных сторон параллельны, все стороны равны по длине и расположены под прямым углом друг к другу, то трапецию можно рассматривать как квадрат
- Если обе пары противоположных сторон параллельны, их противоположные стороны равны по длине и расположены под прямым углом друг к другу, то трапецию можно рассматривать как прямоугольник
Виды трапеций
Есть три типа трапеций, они приведены ниже:
- Равнобедренная трапеция
- Скален трапеция
- Трапеция правая
Равнобедренная трапеция: Если стороны или непараллельные стороны трапеции равны по длине, то она называется равнобедренной трапецией.Углы параллельных сторон (основания) в равнобедренной трапеции равны между собой. Равнобедренная трапеция имеет линию симметрии, и обе диагонали равны по длине.
На приведенной ниже равнобедренной трапеции XYZW, XY и WZ называются основаниями трапеции. WX и YZ называются сторонами трапеции, поскольку они не параллельны друг другу.
Scalene Trapezoid: Если ни стороны, ни углы трапеции не равны, то это разносторонняя трапеция.В приведенной ниже разносторонней трапеции все четыре стороны, то есть AB, BC, CD и DA, имеют разную длину. Основания, то есть DC и AB, параллельны друг другу, но имеют разную длину.
Правая трапеция: Правая трапеция, также называемая прямоугольной трапецией, имеет пару прямых углов. Эти виды трапеций используются для оценки площадей под кривой. На правой трапеции внизу или прямоугольной трапеции есть два прямых угла: один в точке D, а другой в точке A.Одна пара противоположных сторон, то есть DC и AB, параллельны друг другу.
Площадь трапеции
Площадь трапеции рассчитывается путем измерения среднего значения параллельных сторон и умножения его на высоту.
Площадь трапеции рассчитывается по следующей формуле:
Площадь = [(AB + CD) / 2] x
в час.
Где AB и CD — параллельные стороны, а h — высота
Периметр трапеции
Периметр трапеции равен сумме всех ее сторон.Если A, B, C, D — четыре стороны трапеции, то формула периметра:
Периметр = AB + BC + CD + AD
Связанные темы о трапеции
Ниже перечислены несколько тем, относящихся к трапеции.
Что такое трапеции?
Трапеция — это четырехсторонняя замкнутая двухмерная форма, имеющая площадь и периметр. Его еще называют Трапецией. Стороны трапеции параллельны друг другу, и они называются основаниями трапеции.Непараллельные стороны известны как ноги или боковые стороны трапеции. Кратчайшее расстояние между двумя параллельными сторонами называется высотой.
Как найти площадь трапеции?
Площадь трапеции рассчитывается путем вычисления среднего значения двух параллельных сторон и умножения его на высоту.
Площадь = [(a + b) / 2] x h, где a и b — длины оснований, а h — высота.
Что такое уравнение трапеции?
Есть два уравнения для трапеции.Одно уравнение вычисляет его площадь; другой по периметру. Периметр трапеции PQRS задается как Perimeter = PQ + QR + RS + PS. Площадь трапеции = [(a + b) / 2] x h, где a и b — длины оснований, а h — высота.
Трапеция — четырехугольник?
Поскольку у трапеции четыре стороны, она автоматически становится четырехугольником. У него две стороны, которые параллельны, и две стороны, которые не параллельны.
Каковы три атрибута трапеции?
Три основных атрибута трапеции:
- Его базовые углы и диагонали равны, если трапеция равнобедренная
- Точка пересечения диагоналей коллинеарна (на одной прямой) с серединами двух противоположных сторон
- Противоположные стороны равнобедренной трапеции равны
Как найти недостающую сторону трапеции?
Отсутствующая сторона трапеции может быть определена на основании предоставленной вам информации.В случае, если у вас есть площадь и длина оснований, вы можете найти длину по высоте. Вы также можете определить длину отсутствующей стороны, если знаете периметр и длину трех других сторон трапеции.
Равны ли диагонали трапеции?
Трапеции бывают трех видов — Равнобедренная, Скаленовая и Правая. В случае равнобедренной трапеции диагонали равны, так как непараллельные части трапеции равны по длине.В случае разносторонней и правой трапеции диагонали не равны.
фигур в реальной жизни | Треугольники в жизни
Формы в реальной жизни
Эти геометрические фигуры в реальной жизни так приятно видеть, а иногда и главное узнавание объекта.
Источник: giphy.com
Все фигуры, как двухмерные, так и трехмерные, невероятно важны в контексте изучения математики. Основу геометрии составляют эти формы, и когда дети учатся на примерах, они запоминают это навсегда.Давайте посмотрим на некоторые формы в реальной жизни и на то, что мы наблюдали вокруг себя:
Шестиугольник в реальной жизни
Шестиугольники обычно представляют собой шесть прямых сторон равной длины. В этом узоре вы можете увидеть снежинки. Ульи, кристаллы льда — другие частые проявления шестиугольника в реальной жизни.
Ромб в реальной жизни
Параллелограмм с равной длиной сторон представляет собой ромб. Ромб в реальной жизни не является широко распространенной формой в природе, он встречается в некоторых кристаллах и дизайнерских воздушных змеях.Но внимательно наблюдайте, вы сможете заметить еще! Ромб в реальной жизни уже кажется дорогим!
Формы воздушного змея в реальной жизни
Как следует из названия, формы воздушного змея в реальной жизни — это формы, похожие на воздушного змея. Где еще вы видите эту фигуру? Сейчас мы можем думать только о Кадзю Катли, что приходит вам на ум?
Реальный параллелограмм
Параллелограмм — это четырехсторонняя фигура с двумя парами параллельных сторон.Ластики для карандашей, клатчи — это параллелограмм в реальной жизни.
Даже некоторые из самых необычных архитектурных построек имеют форму параллелограмма. Насколько странно в них жить?
Квадраты в реальной жизни
Четыре равные прямые стороны с четырьмя прямыми углами чаще всего наблюдаются после круглой / круглой формы! Квадратные штампы, плитка на полу — все это квадраты, которые вы видите вокруг как примеры квадратов в реальной жизни.
Не забудем подставки, шахматную доску, ключи от ноутбука, над которым вы работаете!
Пентагон в реальной жизни
Нетрадиционный, но его можно увидеть в нескольких местах в реальной жизни. Он использовался в уникальных архитектурных творениях для создания эстетически привлекательных фигур.
Форму пятиугольника в реальной жизни можно увидеть и на футбольном мяче!
Треугольники в жизни
Вопрос в том, где в реальной жизни не видно треугольников? Трехсторонняя фигура имеет различные примеры в нашей повседневной жизни.От канцелярских товаров, которые мы используем, до вкусных начо и пиццы, которые мы едим, есть множество примеров треугольников в реальной жизни.
В старину его даже использовали как компас и солнечные часы.
Пирамида в реальной жизни
Пирамиды — это трехмерные фигуры с одной плоской стороной и ребрами, которые сходятся в одной точке. Великая пирамида в Гизе, крыша дома — это пирамида в реальной жизни, которую вы, возможно, уже заметили!
Если вы заметили, некоторые пирамиды в реальной жизни также пересекаются с треугольниками.
Реальные формы конуса
Рожок мороженого, наполненный сферическими шариками липкой забавы, — наша супер любимая форма. В конце концов, это тоже наш любимый десерт!
А что насчет шляп для вечеринок, которые идеально сидят на наших головах, пока все ждут, когда придут праздничный торт?
Даже ярко-оранжевые дорожные конусы трудно не заметить, когда в реальной жизни видишь конусы формы.
Трапеция в реальной жизни
Все, что происходит в фильме, в какой-то момент содержало трапецию в реальной жизни.Четырехсторонняя фигура с одной парой параллельных сторон — это то, из чего сделана коробка для попкорна.
После этого примера мы больше никогда не забудем трапецию!
И никто не может устоять перед взглядом на блестящий золотой слиток, который в реальной жизни определенно представляет собой трапецию.
Вы можете найти другие наши блоги здесь:
Сводка
Некоторые очень разные формы в природе и геометрические формы в реальной жизни нас удивили.Нам очень нравится видеть трехмерные фигуры в реальной жизни и то, насколько каждая из них по-своему уникальна. Хотя мы можем знать о шестиугольнике в реальной жизни, треугольниках в реальной жизни, ромбах в реальной жизни, квадратах в реальной жизни, параллелограммах в реальной жизни и других геометрических формах в реальной жизни, все они окружают нас своей красотой.

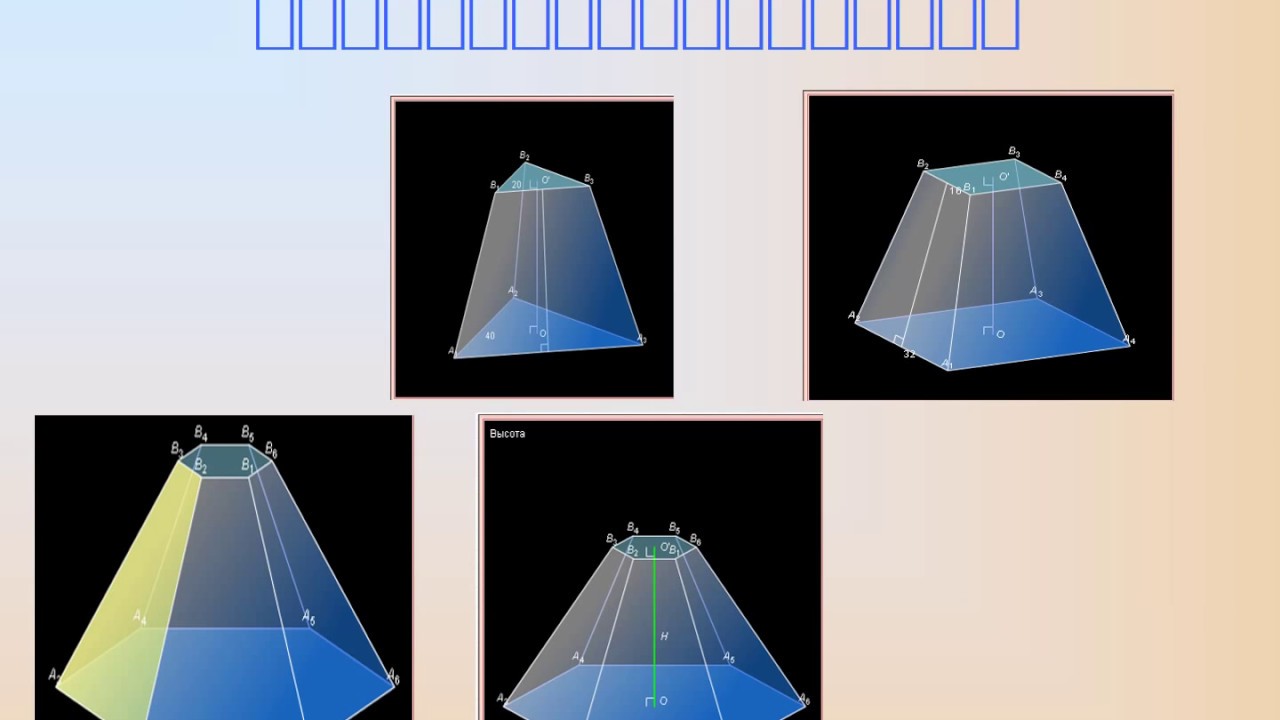

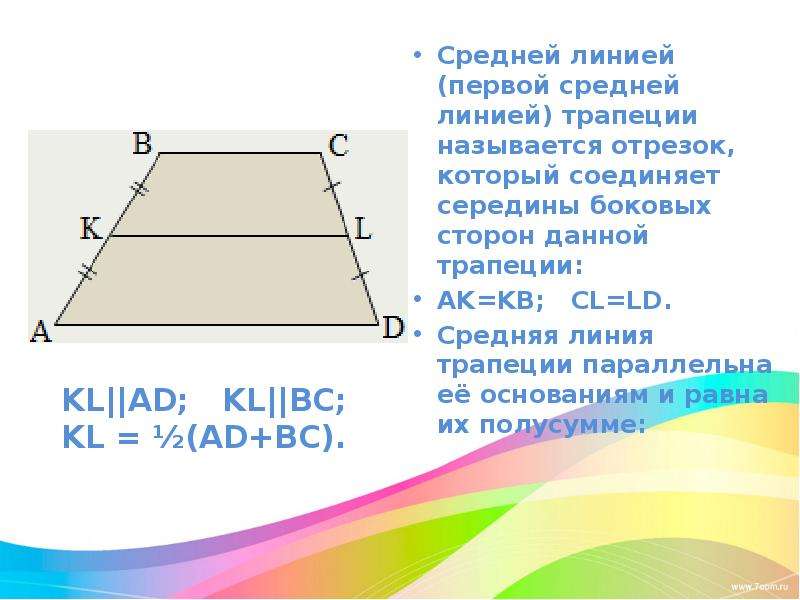


 Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
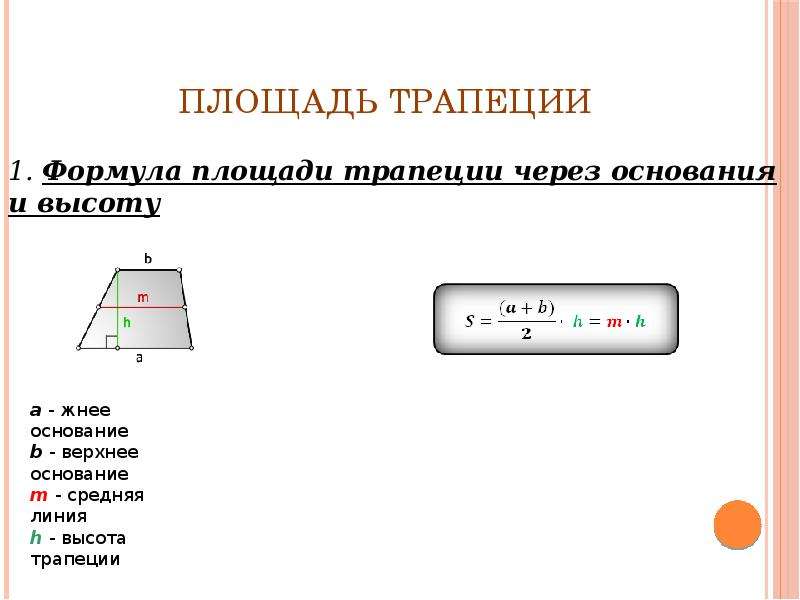
 Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ
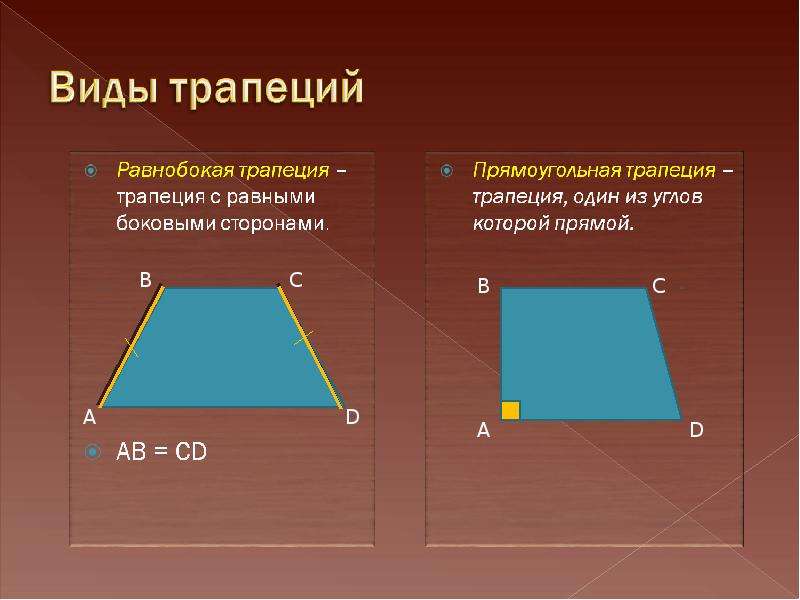 Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2
Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).